
题目列表(包括答案和解析)
(11)命题“存在x∈R,使得x2+2x+5=0”的否定是
(12)抛物线y2=8x的焦点坐标是
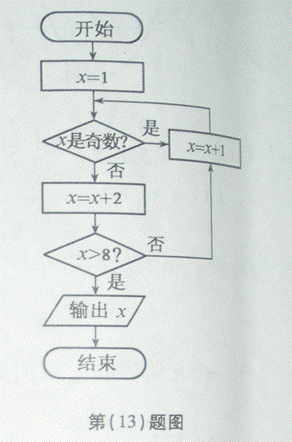
(13)如图所示,程序框图(算法流程图)的输出值x=
(14)某地有居民100000户,其中普通家庭99 000户,高收入家庭1 000户.从普通家庭中以简单随机抽样方式抽取990户,从高收入家庭中以简单随机抽样方式抽取l00户进行调查,发现共有120户家庭拥有3套或3套以上住房,其中普通家庭50户,高收人家庭70户.依据这些数据并结合所掌握的统计知识,你认为该地拥有3套或3套以上住房的家庭所占比例的合理估计是 .
(15)若a>0 ,b>0,a+b=2,则下列不等式对一切满足条件的a.
,b>0,a+b=2,则下列不等式对一切满足条件的a.
b恒成立的是 (写出所有正确命题的编号).
①ab≤1; ②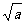 +
+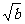 ≤
≤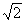 ; ③a2+b2≥2;
; ③a2+b2≥2;
④a3+b3≥3; 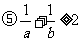
(1)若A=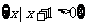 ,B=
,B=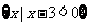 ,则
,则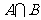 =
=
(A)(-1,+∞) (B)(-∞,3) (C)(-1,3) (D)(1,3)
(2)已知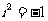 ,则i(
,则i(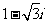 )=
)=
(A)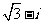 (B)
(B)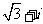 (C)
(C)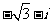 (D)
(D)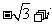
(3)设向量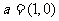 ,
,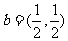 ,则下列结论中正确的是
,则下列结论中正确的是
(A)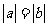 (B)
(B)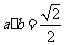
(C)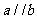
 (D)
(D) 与
与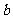 垂直
垂直
(4)过 点(1,0)且与直线x-2y-2=0平行的直线方程是
点(1,0)且与直线x-2y-2=0平行的直线方程是
(A)x-2y-1=0 (B)x-2y+1=0
(C)2x+y-2=0 (D)x+2y-1=0
(5)设数列{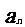 }的前n项和
}的前n项和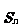 =
=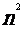 ,则
,则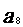 的值为
的值为
(A) 15 (B) 16 (C) 49 (D)64
(6)设abc>0,二次函数f(x)=a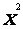 +bx+c的图像可能是
+bx+c的图像可能是

(7)设a= ,b=
,b=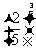 ,c=
,c=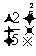 ,则a,b,c的大小关系是
,则a,b,c的大小关系是
(A)a>c>b (B)a>b>c (C)c>a>b (D)b>c>a
(8)设x,y满足约束条件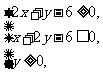 则目标
则目标 函数z=x+y的最大值是
函数z=x+y的最大值是
(A)3 (B) 4 (C) 6 (D)8
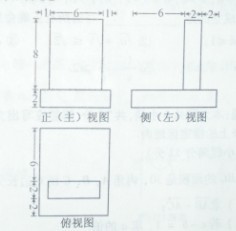
(9)一个几何体的三视图如图,该几何体的表面积是
(A)372 (C)292
(B)360 (D)280

(10)甲从正方形四个顶点中任意选择两个顶点连成直线,一页从该正方形四个顶点中任意选择连个顶点连成直线,则所得的两条直线相互垂直的概率是
(A)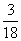
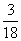 (A)
(A)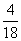 (A)
(A)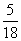
 (A)
(A)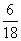
数 学(文科)(安徽卷)
第Ⅱ卷(非选择题共100分)
请用0 5毫米黑色墨水签字笔在答题卡上作答,在试题卷上大体无效。
22.(本小题满分14分)
已知函数f(x)=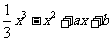 的图像在点P(0,f(0))处的切线方程为y=3x-2
的图像在点P(0,f(0))处的切线方程为y=3x-2
(Ⅰ)求实数a,b的值;
(Ⅱ)设g(x)=f(x)+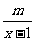 是[
是[ ]上的增函数。
]上的增函数。
(i)求实数m的最大值;
(ii)当m取最大值时,是否存在点Q,使得过点Q的直线若能与曲线y=g(x)围成两个封闭图形,则这两个封闭图形的面积总相等?若存在,求出点Q的坐标;若不存在,说明理由。
21.(本小题满分12分)
某港口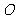 要将一件重要物品用小艇送到一艘正在航行的轮船上,在小艇出发时,轮船位于港口
要将一件重要物品用小艇送到一艘正在航行的轮船上,在小艇出发时,轮船位于港口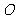 北偏西30°且与该港口相距20海里的
北偏西30°且与该港口相距20海里的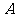 处,并正以30海里/小时的航行速度沿正东方向匀速行驶。假设该小艇沿直线方向以
处,并正以30海里/小时的航行速度沿正东方向匀速行驶。假设该小艇沿直线方向以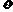 海里/小时的航行速度匀速行驶,经过
海里/小时的航行速度匀速行驶,经过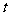 小时与轮船相遇。
小时与轮船相遇。
(Ⅰ)若希望相遇时小艇的航行距离最小,则小艇航行速度的大小应为多少?
(Ⅱ)为保证小艇在30分钟内(含30分钟)能与轮船相遇,试确定小艇航行速度的最小值;
(Ⅲ)是否存在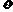 ,使得小艇以
,使得小艇以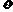 海里/小时的航行速度行驶,总能有两种不同的航行方向与轮船相遇?若存在,试确定
海里/小时的航行速度行驶,总能有两种不同的航行方向与轮船相遇?若存在,试确定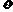 的取值范围;若不存在,请说明理由。
的取值范围;若不存在,请说明理由。
20. (本小题满分12分)
如图,在长方体ABCD – A1B1C1D1中,E,H分别是棱A1B1,D1C1上的点(点E与B1不重合),且EH//A1D1。过EH的平面与棱BB1,CC1相交,交点分别为F,G。
(I)证明:AD//平面EFGH;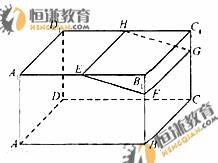
(II)设AB=2AA1=2a。在长方体ABCD-A1B1C1D1内随机选取一点,记该点取自于几何体A1ABFE – D1DCGH内的概率为p。当点E,F分别在棱A1B1, B1B上运动且满足EF=a时,求p的最小值。
19.(本小题满分12分)
已知抛物线C: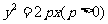 过点A (1 , -2)。
过点A (1 , -2)。
(I)求抛物线C 的方程,并求其准线方程;
(II)是否存在平行于OA(O为坐标原点)的直线L,使得直线L与抛物线C有公共点,且直线OA与L的距离等于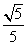 ?若存在,求直线L的方程;若不存在,说明理由。
?若存在,求直线L的方程;若不存在,说明理由。
18.(本小题满分12分)
设平顶向量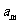 = ( m , 1),
= ( m , 1), 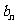 = ( 2 , n ),其中 m, n
= ( 2 , n ),其中 m, n 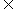 {1,2,3,4}.
{1,2,3,4}.
(I)请列出有序数组( m,n )的所有可能结果;
(II)记“使得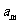
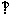 (
(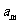 -
-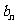 )成立的( m,n )”为事件A,求事件A发生的概率。
)成立的( m,n )”为事件A,求事件A发生的概率。
17. (本小题满分12分 )
数列{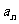 } 中
} 中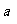 =
=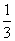 ,前n项和
,前n项和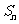 满足
满足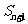 -
-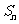 =
=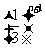 (n
(n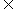
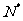 ).
).
( I ) 求数列{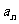 }的通项公式
}的通项公式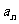 以及前n项和
以及前n项和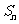 ;
;
(II)若S1, t ( S1+S2 ), 3( S2+S3 ) 成等差数列,求实数t的值。
16. 观察下列等式:
①
cos2a=2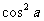 -1;
-1;
② cos4a=8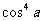 - 8
- 8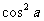 + 1;
+ 1;
③ cos6a=32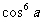 - 48
- 48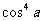 + 18
+ 18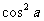 - 1;
- 1;
④ cos8a=128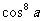 - 256
- 256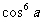 + 160
+ 160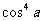 - 32
- 32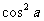 + 1;
+ 1;
⑤ cos10a=
m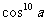 - 1280
- 1280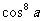 + 1120
+ 1120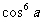 + n
+ n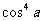 + p
+ p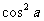 - 1.
- 1.
可以推测,m – n + p = .
15. 对于平面上的点集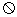 ,如果连接
,如果连接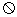 中任意两点的线段必定包含于
中任意两点的线段必定包含于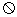 ,则称
,则称 为平面上的凸集,给出平面上4个点集的图形如下(阴影区域及其边界):
为平面上的凸集,给出平面上4个点集的图形如下(阴影区域及其边界):
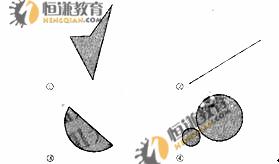
其中为凸集的是 (写出所有凸集相应图形的序号)。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com