4.若f(x)是R上的减函数,且f(0)＝3,f(3)＝-1.设P＝{x||f(x+t)-1|＜2},Q＝{x|f(x)＜-1},若“x∈P”是“x∈Q”的充分不必要条件,则实数t的取值范围是(　　 )

A.t≤0　 　　　　　　　　　B.t≥0 　　　　　　　　　C.t≤-3　　 　　　　　　　D.t≥-3

解析:由题意知P＝{x|-1＜f(x+t)＜3}＝{x|-t＜x＜3-t},Q＝{x|f(x)＜f(3)}＝{x|x＞3},

∵“x∈P”是“x∈Q”的充分而不必要条件,

∴P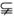Q.∴-t≥3,t≤-3.故选C.

答案:C

3.对任意实数a、b、c,给出下列命题:

①“a＝b”是“ac＝bc”的充要条件;

②“a+5是无理数”是“a是无理数”的充要条件;

③“a＞b”是“a²＞b²”的充分条件;

④“a＜5”是“a＜3”的必要条件.

其中真命题的个数是(　　 )

A.1　　　　　 　　　　　B.2 　　　　　　　　　　　　C.3　 　　　　　　　　　D.4

解析:当c＝0,a、b不为0时,ac≠bc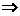a＝b,所以①是假命题;当a＝2,b＝-3时,a＞b推不出a²＞b²,所以③是假命题;②④显然正确.

答案:B

2.(2008重庆高考,文2)设x是实数,则“x＞0”是“|x|＞0”的(　　 )

A.充分而不必要条件　　　　 　　　　　　　　　　　　　B.必要而不充分条件

C.充要条件　　　　　　　　　 　　　　　　　　　　　　D.既不充分也不必要条件

解析:由x＞0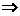|x|＞0充分,而|x|＞0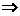x＞0或x＜0,不必要,故选A.

答案:A

1.全称命题“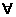x∈Z,2x+1是整数”的逆命题是(　　 )

A.若2x+1是整数,则x∈Z　　　　　　　　　　　　　　　 B.若2x+1是奇数,则x∈Z

C.若2x+1是偶数,则x∈Z　　　　　　　　　　　　　　　 D.若2x+1能被3整除,则x∈Z

解析:命题“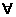x∈Z,2x+1是整数”的条件为x∈Z,结论为2x+1是整数,故选A.

答案:A

12.已知定义域为R的单调函数f(x)满足f(x+y)＝f(x)+f(y),且f(1)＝2.

(1)判断f(x)的奇偶性和单调性；

(2)解不等式f(x²-2x)+f(2-x)＞0;

(3)若f(klog₂t)+f(log₂t-(log₂t)²-2)＜0对t∈(0,+∞)恒成立.求实数k的取值范围.

解:(1)令x＝y＝0,得f(0)＝0.

令y＝-x,得f(0)＝f(x)+f(-x)＝0.

∴f(-x)＝-f(x).

∴f(x)为奇函数.

又f(0)＝0,f(1)＝2,f(x)在R上是单调函数,

故由f(0)＜f(1),知f(x)在R上是单调递增函数.

(2)不等式f(x²-2x)+f(2-x)＞0,即f(x²-2x)＞-f(2-x).

由(1),知f(x²-2x)＞f(x-2).

∴x²-2x＞x-2,即x²-3x+2＞0.

解得x∈(-∞,1)∪(2,+∞).

(3)f(klog₂t)+f(log₂t-(log₂t)²-2)＜0对t∈(0,+∞)恒成立,

即f(klog₂t)＜-f(log₂t-(log₂t)²-2)对t∈(0,+∞)恒成立,

即f(klog₂t)＜f(-log₂t+(log₂t)²+2)对t∈(0,+∞)恒成立.

由f(x)在R上是单调递增函数，得klog₂t＜-log₂t+(log₂t)²+2对t∈(0,+∞)恒成立,

即(log₂t)²-(k+1)log₂t+2＞0对t∈(0,+∞)恒成立.

由t∈(0,+∞),知log₂t∈(-∞,+∞).

令m＝log₂t,则m∈(-∞,+∞),m²-(k+1)m+2＞0对m∈(-∞,+∞)恒成立.

∴Δ＝(k+1)²-8＜0,解得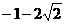＜k＜.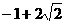

11.解关于x的不等式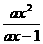＞x(a∈R).

解:原不等式可化为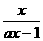＞0，等价于x(ax-1)＞0.

当a＞0时，不等式的解集为{x|x＜0或x＞};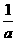

当a＜0时，不等式的解集为{x|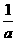＜x＜0};

当a＝0时，不等式的解集为{x|x＜0}.

10.若函数f(x)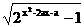＝的定义域为R,则a的取值范围为.

解析: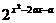≥1＝2⁰恒成立x²-2ax-a≥0恒成立Δ＝(2a)²+4a≤0a(a+1)≤0,

∴-1≤a≤0.

答案:［-1,0］

9.(2008江西高考，理14)不等式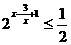的解集为__________________.

解析:

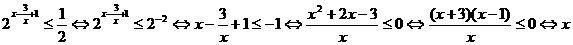∈(-∞,-3］∪(0,1］.

答案:(-∞,-3］∪(0,1］

8.(2008山东高考，理16)若不等式|3x-b|＜4的解集中的整数有且仅有1,2,3,则b的取值范围为_____________________.

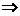
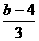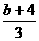
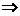
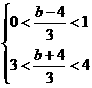
解析:由|3x-b|＜4＜x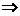＜5＜b＜7,即b的取值范围为(5,7).

答案:(5,7)

7.已知关于x的不等式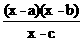≥0的解集为{x|-3≤x＜-2或x≥4}，则点(a+b,c)位于坐标平面内(　　 )

A.第一象限　　　　　 B.第二象限　　　　　　 C.第三象限　　　　　　 D.第四象限

解析:由数轴标根法可知c＝-2,a+b＝1，因此(a+b,c)位于坐标平面内的第四象限.

答案:D