
题目列表(包括答案和解析)
19. (理)(Ⅲ)同解法一
19.(Ⅰ)解,依题意每年投入构成首项为800万元,公比为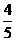 的等比数列,每年旅游业收入组织首项为400万元,公比为
的等比数列,每年旅游业收入组织首项为400万元,公比为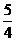 的等比数列。………………………………2分
的等比数列。………………………………2分
所以,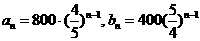 ………………………………4分
………………………………4分
(Ⅱ)解,经过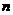 年,总收投入
年,总收投入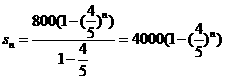 ………5分
………5分
经过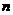 年,总收入
年,总收入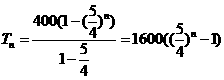 ……………6分
……………6分
设经过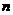 年,总收入超过总投入,由此,
年,总收入超过总投入,由此,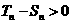 ,
,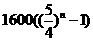
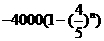

化简得 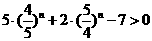 ………………………………8分
………………………………8分
设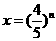 代入上式整理得,
代入上式整理得,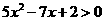
解得,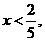 或
或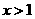 (舍去)………………………………10分
(舍去)………………………………10分
由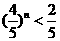 ,
,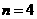 时,
时,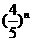
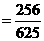
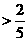 ,
,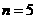 ,
,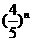 =
=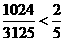 ………12分
………12分
因为 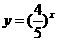 在定义域上是减函数,所以
在定义域上是减函数,所以 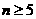 ……………………13分
……………………13分
答:至少经过5年旅游业的总收入超过总投入。………………………………14分
19. (本题满分14分)
从社会效益和经济效益出发,某地投入资金进行生态环境建设,并以此发展旅游产业,打算本年度投入800万元,以后每年投入将比上年平均减少 ,本年度旅游收入为400万元,由于该项建设对旅游的促进作用,预计今后的旅游业收入每年会比上年平均增加
,本年度旅游收入为400万元,由于该项建设对旅游的促进作用,预计今后的旅游业收入每年会比上年平均增加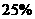 .
.
(Ⅰ)设第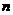 年(本年度为第一年)的投入为
年(本年度为第一年)的投入为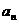 万元,旅游业收入为
万元,旅游业收入为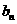 万元,写出
万元,写出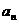 ,
,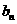 的表达式;
的表达式;
(Ⅱ)至少经过几年旅游业的总收入超过总投入?
21. [解析](1)令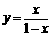 ,解得
,解得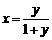 ,由
,由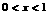 ,解得
,解得 ,
,
∴函数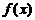 的反函数
的反函数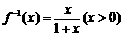 ,则
,则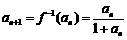 ,得
,得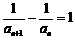 .
.
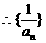 是以2为首项,l为公差的等差数列,故
是以2为首项,l为公差的等差数列,故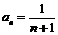 .
……3分
.
……3分
(2)∵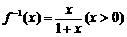 ,∴
,∴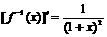 ,
,
∴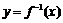 在点
在点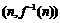 处的切线方程为
处的切线方程为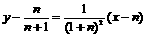 ,
,
令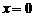 , 得
, 得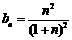 ,∴
,∴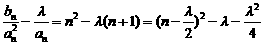 ,
,
∵仅当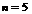 时取得最小值,∴
时取得最小值,∴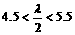 ,解之
,解之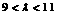 ,
,
∴的取值范围为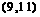 .
……7分
.
……7分
(3)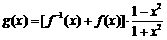
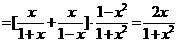 ,
,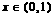 .
.
则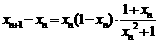 ,
,
因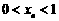 ,则
,则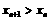 ,显然
,显然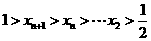 .
.
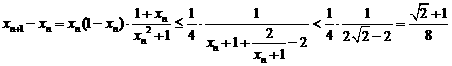
∴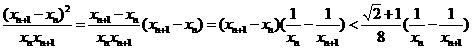
∴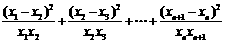
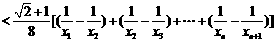
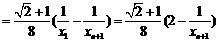
∵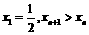 ,∴
,∴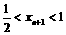 ,
,
∴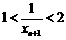 ,∴
,∴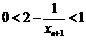
∴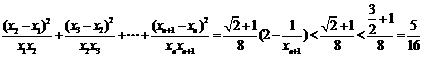 . ……12分
. ……12分
21.(本小题满分12分)已知函数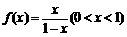 的反函数为
的反函数为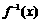 ,数列
,数列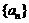 和
和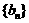 满足:
满足: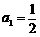 ,
,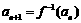 ,函数
,函数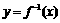 的图象在点
的图象在点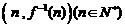 处的切线在轴上的截距为
处的切线在轴上的截距为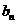 .
.
(1)求数列{ }的通项公式;
}的通项公式;
(2)若数列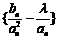 的项仅
的项仅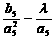 最小,求的取值范围;
最小,求的取值范围;
(3)令函数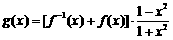 ,
,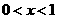 ,数列
,数列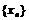 满足:
满足: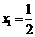 ,
,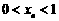 ,且
,且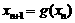 ,其中
,其中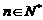 .证明:
.证明: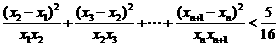 .
.
20.解:(Ⅰ)因为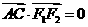 ,所以有
,所以有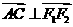
所以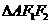 为直角三角形;
为直角三角形;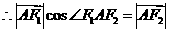 …………………………2分
…………………………2分
则有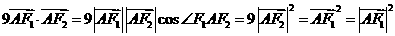
所以,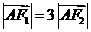 …………………………3分
…………………………3分
又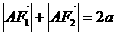 ,
,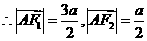 ………………………4分
………………………4分
在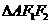 中有
中有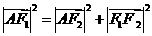
即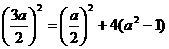 ,解得
,解得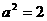
所求椭圆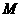 方程为
方程为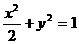 …………………………6分
…………………………6分
(Ⅱ)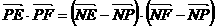
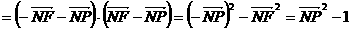
从而将求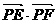 的最大值转化为求
的最大值转化为求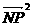 的最大值
…………………8分
的最大值
…………………8分
是椭圆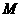 上的任一点,设
上的任一点,设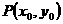 ,则有
,则有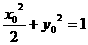 即
即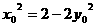
又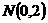 ,所以
,所以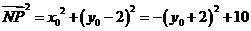 ………………10分
………………10分
而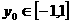 ,所以当
,所以当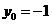 时,
时,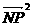 取最大值
取最大值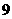
故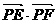 的最大值为
的最大值为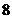 ……………………12分
……………………12分
20.(本小题满分12分)已知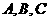 均在椭圆
均在椭圆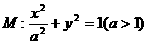 上,直线
上,直线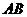 、
、 分别过椭圆的左右焦点
分别过椭圆的左右焦点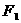 、
、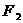 ,当
,当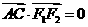 时,有
时,有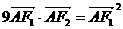 .
.
(Ⅰ)求椭圆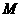 的方程;
的方程;
(Ⅱ)设是椭圆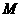 上的任一点,
上的任一点,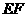 为圆
为圆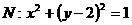 的任一条直径,求
的任一条直径,求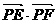 的最大值.
的最大值.
19.解:(Ⅰ)已知函数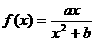 ,
,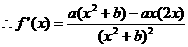 …………1分
…………1分
又函数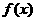 在
在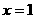 处取得极值2,
处取得极值2,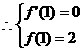 …………2分
…………2分
即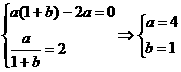
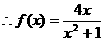 …………………4分
…………………4分
(Ⅱ)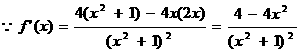 由
由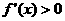 ,得
,得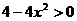 ,即
,即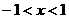
所以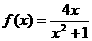 的单调增区间为(-1,1) ………………… 6分
的单调增区间为(-1,1) ………………… 6分
因函数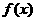 在(m,2m+1)上单调递增,
在(m,2m+1)上单调递增,
则有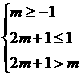 , …………7分
, …………7分
解得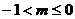 即
即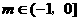 时,函数
时,函数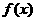 在(m,2m+1)上为增函数 ………8分
在(m,2m+1)上为增函数 ………8分
(Ⅲ)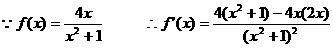
直线l的斜率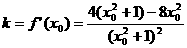 …………9分
…………9分
即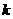
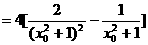 令
令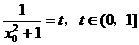 , …………10分
, …………10分
则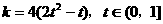
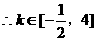 即直线l的斜率k的取值范围是
即直线l的斜率k的取值范围是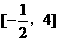 ……………12分
……………12分
19.(本小题满分12分)已知函数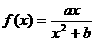 ,在
,在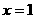 处取得极值为.
处取得极值为.
(Ⅰ)求函数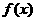 的解析式;
的解析式;
(Ⅱ)若函数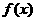 在区间
在区间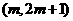 上为增函数,求实数的取值范围;
上为增函数,求实数的取值范围;
(Ⅲ)若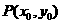 为
为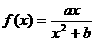 图象上的任意一点,直线
图象上的任意一点,直线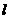 与
与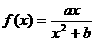 的图象相切于点,求直线
的图象相切于点,求直线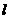 的斜率的取值范围.
的斜率的取值范围.
19.(本小题满分12分)
某沿海地区养殖的一种特色海鲜上市时间仅能持续5个月,预测上市初期和后期会因供不应求使价格呈持续上涨态势,而中期又将出现供大于求使价格连续下跌.现有三种价格模拟函数:①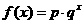 ;②
;②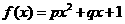 ;③
;③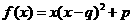 .(以上三式中、均为常数,且
.(以上三式中、均为常数,且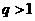 )
)
(I)为准确研究其价格走势,应选哪种价格模拟函数,为什么?
(II)若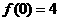 ,
,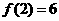 ,求出所选函数
,求出所选函数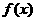 的解析式(注:函数定义域是
的解析式(注:函数定义域是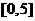 .其中
.其中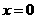 表示8月1日,
表示8月1日,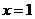 表示9月1日,…,以此类推);
表示9月1日,…,以此类推);
(III)为保证养殖户的经济效益,当地政府计划在价格下跌期间积极拓宽外销,请你预测该海鲜将在哪几个月份内价格下跌.
解:(I)根据题意,应选模拟函数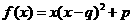 2分
2分
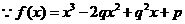 ,
,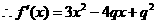 3分
3分
 若
若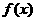 ≥
≥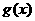 恒成立,即
恒成立,即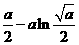 ≥
≥ 恒成立
恒成立
解之得≤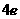 .
10分
.
10分
(III)由(II)得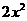 ≥
≥ ,即
,即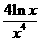 ≤
≤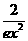 11分
11分
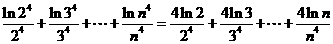
≤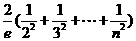
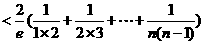 12分
12分
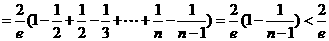 13分
13分
 所以
所以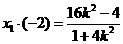 ,得
,得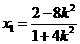 9分
9分
所以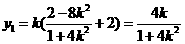
所以直线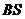 的斜率为
的斜率为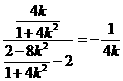 ,
10分
,
10分
则直线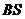 的方程可设为
的方程可设为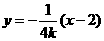
由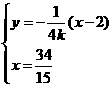 ,得
,得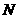 点的坐标为
点的坐标为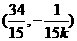 12分
12分
所以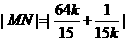 ≥
≥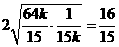
当且仅当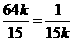 即
即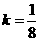 时取等号.
14分
时取等号.
14分
(20)(本小题满分12分)
已知数列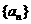 的前
的前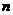 项和为
项和为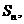 且
且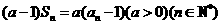 。
。
(Ⅰ)求证数列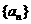 是等比数列,并求
是等比数列,并求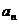 ;
;
(Ⅱ)已知集合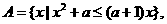 问是否存在实数
问是否存在实数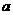 ,使得对于任意的
,使得对于任意的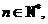 都有
都有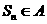 ?若存在,求出
?若存在,求出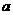 的取值范围;若不存在,说明理由。
的取值范围;若不存在,说明理由。
(20)解:(Ⅰ)当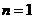 时,
时, 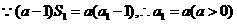 …………………………1分
…………………………1分
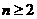 时,由
时,由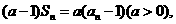 得
得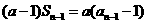
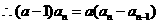 ,变形得:
,变形得: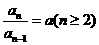 ………………………………………4分
………………………………………4分
故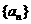 是以
是以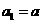 为首项,公比为
为首项,公比为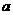 的等比数列,
的等比数列,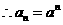 ………………………………6分
………………………………6分
(Ⅱ)(1)当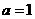 时,
时,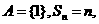 只有
只有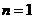 时
时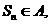
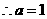 不适合题意
……………………………………………………7分
不适合题意
……………………………………………………7分
(2)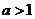 时,
时,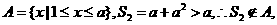
即当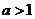 时,不存在满足条件的实数
时,不存在满足条件的实数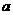 ………………………………………………………9分
………………………………………………………9分
(3)当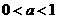 时,
时,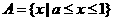
而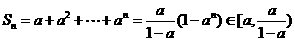
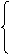 因此对任意的
因此对任意的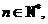 要使
要使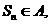 只需
只需 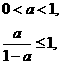 解得
解得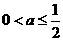 ………………………11分
………………………11分
综上得实数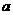 的范围是
的范围是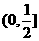 ……………………………………………………12分
……………………………………………………12分
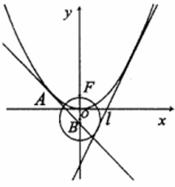 (21)(本小题满分12分)
(21)(本小题满分12分)
已知抛物线 的方程是
的方程是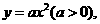 圆
圆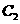 的方程是
的方程是
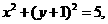 直线
直线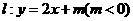 是
是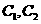 的公切
的公切
线,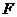 是
是 的焦点.
的焦点.
(Ⅰ)求 与
与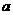 的值;
的值;
(Ⅱ)设 是抛物线
是抛物线 上的一动点,以
上的一动点,以 为切点作
为切点作 的
的
切线交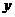 轴于点
轴于点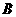 ,若
,若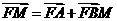 ,则点
,则点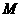 在一定直线上,试证明之。
在一定直线上,试证明之。
(21)解:(Ⅰ)由己知,圆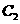 的圆心为
的圆心为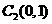 ,半径
,半径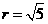
由题设圆心到直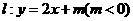 的距离
的距离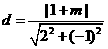
即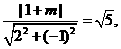 解得
解得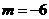 (
(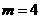 舍去)…………………………………………3分
舍去)…………………………………………3分
设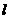 与抛物线相切的切点为
与抛物线相切的切点为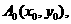 又
又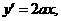 得
得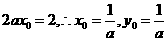
代入直线方程,得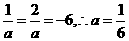 ……………………6分
……………………6分
所以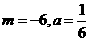
(Ⅱ)由(Ⅰ)知抛物线 的方程为
的方程为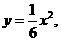 焦点
焦点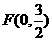
设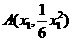 ,由(Ⅰ)知以
,由(Ⅰ)知以 为切点的切线方程为
为切点的切线方程为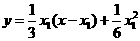 …………8分
…………8分
令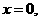 得点
得点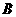 的坐标为
的坐标为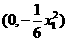
所以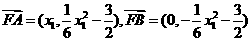 ……………………………………………10分
……………………………………………10分
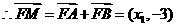 ,因
,因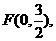 设
设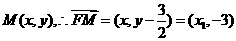
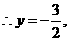 即
即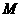 点在定直线
点在定直线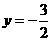 上 ……………………………………………………12分
上 ……………………………………………………12分
(22)(本小题满分14分)
己知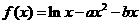 。
。
(Ⅰ)若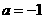 ,函数
,函数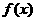 在其定义域内是增函数,求
在其定义域内是增函数,求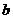 的取值范围;
的取值范围;
(Ⅱ)当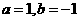 时,证明函数
时,证明函数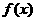 只有一个零点;
只有一个零点;
(Ⅲ)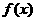 的图象与
的图象与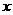 轴交于
轴交于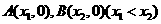 两点
两点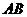 中点为
中点为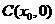 ,求证:
,求证: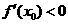 。
。
(22)解:(Ⅰ)依题意: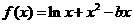
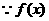 在
在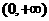 上递增,
上递增,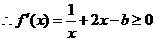 对
对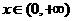 恒成立
恒成立
即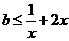 对
对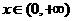 恒成立,
恒成立, 只需
只需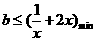 ……………………………2分
……………………………2分
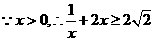 当且仅当
当且仅当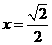 时取
时取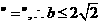 ,
,
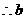 的取值范围为
的取值范围为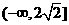 ……………………………………………………………4分
……………………………………………………………4分
(Ⅱ)当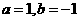 时,
时,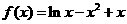 ,其定义域是
,其定义域是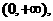
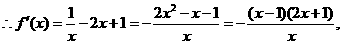 ……………………………………6分
……………………………………6分
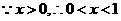 时,
时,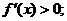 当
当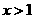 时,
时,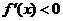
 函数
函数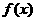 在区间
在区间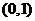 上单调递增,在区间
上单调递增,在区间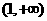 上单调递减
上单调递减
 当
当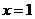 时,函数
时,函数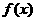 取得最大值,其值为
取得最大值,其值为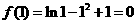
当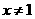 时,
时,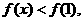 即
即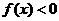
 函数
函数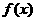 只有一个零点 ……………………………………………………………9分
只有一个零点 ……………………………………………………………9分
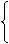
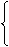 (Ⅲ)由已知得
(Ⅲ)由已知得
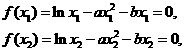
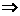
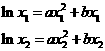 两式相减,得
两式相减,得
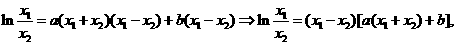 …………11分
…………11分
由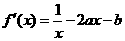 及
及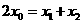 ,得
,得
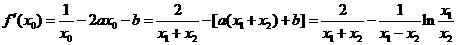
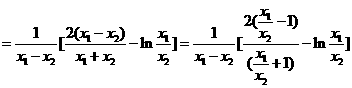 …………………………………12分
…………………………………12分
令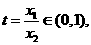 且
且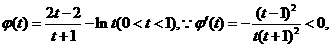
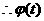 在
在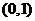 上递减,
上递减,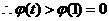
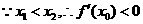 ……………………………………………………………………14分
……………………………………………………………………14分
20.证明:
假设 ∴
∴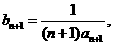 ………1分
………1分
∵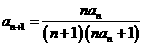 ,
,
∴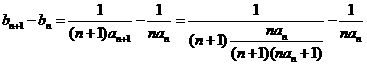 =
=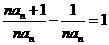
…………………………………3分

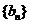 是首项为2,公差为1的等差数列.
………………………………4分
是首项为2,公差为1的等差数列.
………………………………4分

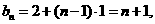
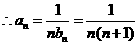 =
=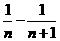 , …………6分
, …………6分
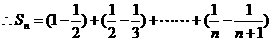 =
= . …………8分
. …………8分
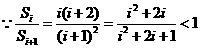 , …………………………………9分
, …………………………………9分
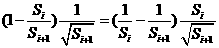
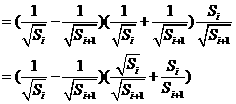
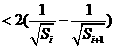 . …………………………………13分
. …………………………………13分


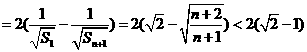 .…………16
.…………16
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com