77.圆与圆关系,常化为圆心距与两圆半径间关系.设圆心距为d,两圆半径分别为r,R,则d>r+R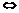两圆相离;d＝r+R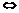两圆相外切;|R－r|<d<r+R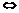两圆相交;d＝|R－r|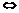两圆相内切;d<|R－r|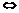两圆内含;d=0,同心圆。

76.直线与圆关系,常化为线心距与半径关系，如：用垂径定理,构造Rt△解决弦长问题，又:d>r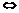相离;d=r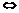相切;d<r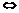相交.

75.若(x₀-a)²+(y₀-b)²<r²(=r²,>r²),则 P(x₀,y₀)在圆(x-a)²+(y-b)²=r²内(上、外)

74.圆:标准方程(x－a)²+(y－b)²=r²;一般方程:x²+y²+Dx+Ey+F=0(D²+E²-4F>0)

参数方程: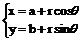;直径式方程(x-x₁)(x-x₂)+(y-y₁)(y-y₂)=0

73.l₁到l₂的角tanθ=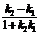;夹角tanθ=|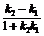|;点线距d=;

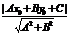72.两直线平行和垂直①若斜率存在l₁:y=k₁x+b₁,l₂:y=k₂x+b₂则l₁∥l₂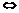k₁∥k₂,b₁≠b₂;l₁⊥l₂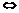k₁k₂=-1

②若l₁:A₁x+B₁y+C₁=0,l₂:A₂x+B₂y+C₂=0,则l₁⊥l₂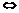A₁A₂+B₁B₂=0_；

③若A₁、A₂、B₁、B₂都不为零l₁∥l₂;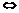

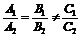④l₁∥l₂则化为同x、y系数后距离d=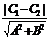

71.直线方程:点斜式 y-y₁=k(x-x₁);斜截式y=kx+b; 一般式:Ax+By+C=0

两点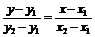式:;截距式: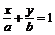(a≠0;b≠0);求直线方程时要防止由于零截距和无斜率造成丢解,直线Ax+By+C=0的方向向量为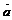=(A,-B)

70.倾斜角α∈[0,π],α=90⁰斜率不存在;斜率k=tanα=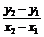

69.三面角公式:AB和平面所成角是θ,AB在平面内射影为AO,AC在平面内,设∠CAO=α,∠BAC=β,则cosβ=cosθcosα;长方体:对角线长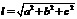;若长方体的体对角线与过同一顶点的三条棱所成角分别为α,β,γ,则有cos²α+cos²β+cos²γ=1;体对角线与过同顶点的三侧面所成角分别为α,β,γ,则cos²α+cos²β+cos²γ=2;正方体和长方体外接球直径=体对角线长;

特别指出：立体几何中平行、垂直关系的证明的基本思路是利用线面关系的转化，即：

68. 常用转化思想:①构造四边形、三角形把问题化为平面问题②将空间图展开为平面图③割补法④等体积转化⑤线线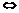平行线面平行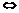面面平行⑥线线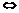垂直线面垂直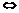面面垂直⑦有中点等特殊点线,用“中位线、重心”转化.