
题目列表(包括答案和解析)
20、(本题13分)过圆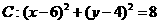 上一点A(4,6)作圆的一条动弦AB,点P为弦AB的中点。
上一点A(4,6)作圆的一条动弦AB,点P为弦AB的中点。
(1)求点P的轨迹方程;
(2)设点P关于点D(9,0)的对称点为E,O为坐标原点,将线段OP绕原点O依逆时针方向旋转90度后,所得线段为OF,求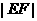 的取值范围。
的取值范围。
19、解:(1)设第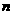 年底该县农村医保基金为
年底该县农村医保基金为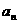 万元,
万元,
则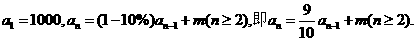 (3分)
(3分)
于是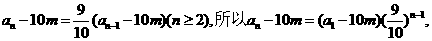
即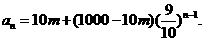 (6分)
(6分)
故第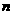 年底该县农村医保基金有
年底该县农村医保基金有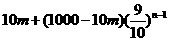 万元。
(7分)
万元。
(7分)
(2)若每年年底的医保基金逐年增加,则数列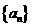 单调递增,
单调递增,
因为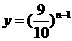 是减函数,则
是减函数,则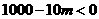 时,即
时,即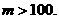 时
(10分)
时
(10分)
又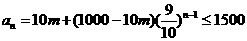 恒成立,则
恒成立,则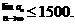
即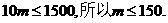 (12分)
(12分)
故每年新增医保基金 的应控制在100万元到150万元之间。
(13分)
的应控制在100万元到150万元之间。
(13分)
19、(本题13分)某县为了贯彻落实党中央国务院关于农村医疗保险(简称“医保”)政策,制定了如下实施方案:2009年底通过农民个人投保和政府财政投入,共集资1000万元作为全县农村医保基金,从2010年起,每年报销农民的医保费都为上一年底医保基金余额的10%,并且每年底县财政再向医保基金注资 万元(
万元( 为正常数)。
为正常数)。
(1)以2009年为第一年,求第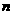 年底该县农村医保基金有多少万元?
年底该县农村医保基金有多少万元?
(2)根据该县农村人口数量和财状况,县政府决定每年年底的医保基金要逐年增加,同时不超过1500万元,求每年新增医保基金 (单位:万元)应控制在什么范围内。
(单位:万元)应控制在什么范围内。
22.解:(Ⅰ)∵OA=[ +2
+2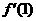 ]OB-
]OB-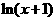 OC,且A、B、C在直线
OC,且A、B、C在直线 上,
上,

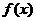 +2
+2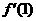 ―
―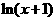 =1, …………(2分)
=1, …………(2分)
 y=
y=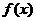 =
=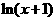 +1-2
+1-2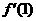 ,
,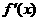 =
=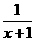 ,于是
,于是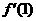 =
=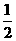 ,
,

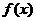 =
=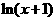 ………(4分)
………(4分)
(Ⅱ)令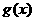 =
=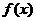 -
-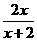 ,由
,由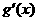 =
=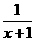 -
-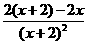 =
=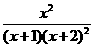 ,
,
以及x>0,知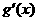 >0,
>0,
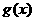 在
在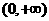 上为增函数,又
上为增函数,又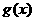 在x=0处右连续,
在x=0处右连续,
 当x>0时,得
当x>0时,得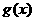 >
>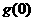 =0,
=0,
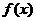 >
>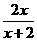 …………(8分)
…………(8分)
(Ⅲ)原不等式等价于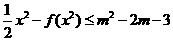 ,
,
令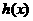 =
= =
=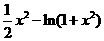 ,则
,则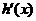 =
=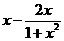 =
=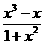 ,(10分)
,(10分)
∵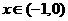 时,
时,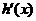 >0,
>0,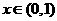 时,
时,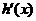 <0,
<0,

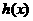 在
在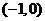 为增函数,在
为增函数,在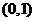 上为减函数,
…………(11分)
上为减函数,
…………(11分)
 当
当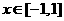 时,
时,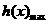 =
= =0,从而依题意有0
=0,从而依题意有0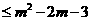 ,
,
解得 ,故m的取值范围是
,故m的取值范围是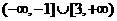 …………(12分)
…………(12分)
22.(本小题满12分)
已知A、B、C是直线l上的三点,O是直线l外一点,向量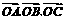 满足
满足
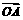 =[f(x)+2f ′(1)]
=[f(x)+2f ′(1)] 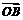 -ln(x+1)
-ln(x+1)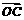
(Ⅰ)求函数y=f(x)的表达式;
(Ⅱ)若x>0,证明:f(x)>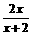 ;
;
(Ⅲ)若不等式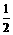 x2≤f(x2)+m2-2m-3对x∈[-1,1]恒成立,求实数m的取值范围.
x2≤f(x2)+m2-2m-3对x∈[-1,1]恒成立,求实数m的取值范围.
21.(本题满分12分)解: (Ⅰ)∵椭圆E: 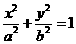 (a,b>0)经过M(-2,
(a,b>0)经过M(-2,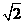 ) ,一个焦点坐标为
) ,一个焦点坐标为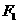 (
( ),∴
),∴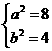 ,椭圆E的方程为
,椭圆E的方程为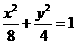 ; …………………4分
; …………………4分
(Ⅱ)当直线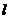 的斜率存在时,设直线
的斜率存在时,设直线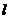 与椭圆E的两个交点为A(
与椭圆E的两个交点为A(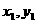 ),B(
),B(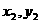 ),相交所得弦的中点
),相交所得弦的中点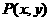 ,∴
,∴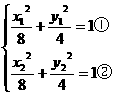 ,
,
①-②得,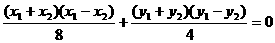 ,
,
∴弦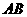 的斜率
的斜率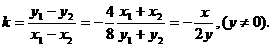 ,
,
∵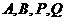 四点共线,∴
四点共线,∴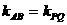 ,即
,即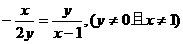 ,
,
经检验(0,0),(1,0)符合条件,
∴线段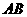 中点
中点 的轨迹方程是
的轨迹方程是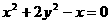 .…………………8分
.…………………8分
(Ⅲ)当⊙ 的切线斜率存在时,设⊙
的切线斜率存在时,设⊙ 的切线方程为
的切线方程为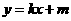 ,
,
由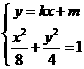 得
得 ,设
,设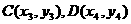 ,则
,则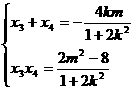 ∵
∵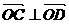 ,∴
,∴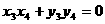 ,即
,即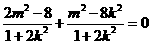 ,
,
∴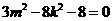 ,即
,即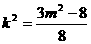 ,∵直线
,∵直线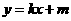 为⊙
为⊙ 的一条切线,
的一条切线,
∴圆的半径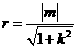 , 即
, 即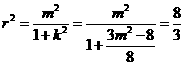 ,
,
经检验,当⊙ 的切线斜率不存在时也成立.∴
的切线斜率不存在时也成立.∴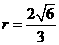 .…………12分
.…………12分
21. (本题满分12分)
已知椭圆E: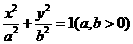 的焦点坐标为
的焦点坐标为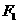 (
( ),点M(
),点M(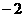 ,
,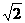 )在椭圆E上.
)在椭圆E上.
(Ⅰ)求椭圆E的方程;
(Ⅱ)设Q(1,0),过Q点引直线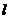 与椭圆E交于
与椭圆E交于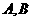 两点,求线段
两点,求线段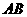 中点
中点 的轨迹方程;(Ⅲ)O为坐标原点,⊙
的轨迹方程;(Ⅲ)O为坐标原点,⊙ 的任意一条切线与椭圆E有两个交点
的任意一条切线与椭圆E有两个交点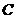 ,
,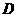 且
且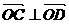 ,求⊙
,求⊙ 的半径.
的半径.
20. (Ⅰ)由题意知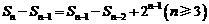 即
即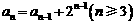
∴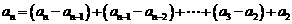
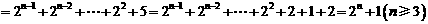
检验知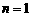 、
、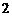 时,结论也成立,故
时,结论也成立,故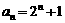 .
.
(Ⅱ)由于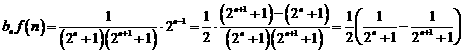
故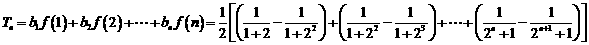
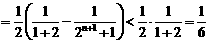 .
.
20. (本题满分12分)
已知数列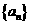 中,
中,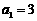 ,
,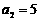 ,其前
,其前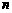 项和
项和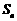 满足
满足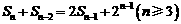 .令
.令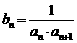 .
.
(Ⅰ)求数列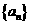 的通项公式;
的通项公式;
(Ⅱ)若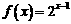 ,求证:
,求证: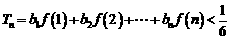 (
( ).
).
22.(本小题满分16分)
解:(1)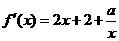
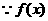 在(0,1)上单调
在(0,1)上单调
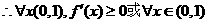
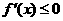 (这是城“=”只对个别
(这是城“=”只对个别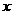 成立)
成立)
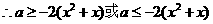
从而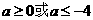 7分
7分
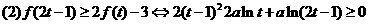 ①
①
令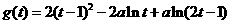
则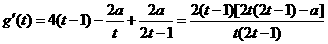
当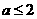 时
时
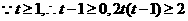
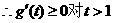 恒成立,
恒成立,
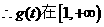 上递增,
上递增,
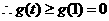 ,即1式对
,即1式对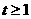 恒成立。
恒成立。
当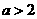 时,
时,
令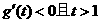 ,
,
解得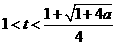
于是,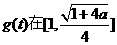 上递减,在
上递减,在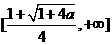 上递增,
上递增,
从而有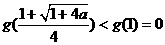 ,即①式不可能恒成立。
,即①式不可能恒成立。
综上所述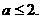 16分
16分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com