
题目列表(包括答案和解析)
8.若函数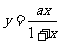 的图像关于直线
的图像关于直线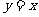 对称,则
对称,则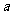 为
为
A.1
B.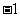 C.
C. D.任意实数
D.任意实数
7.等比数列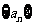 中,
中,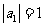 ,
, ,
,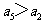 ,则
,则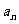
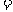
A.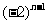 B.
B.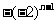 C.
C.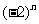 D.
D.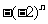
6.函数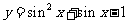 的值域为
的值域为
A.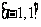 B.
B.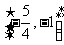 C.
C.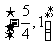 D.
D.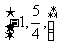
5.不等式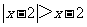 的解集是
的解集是
A.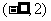 B.
B. C.
C. D.
D.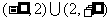
4.若函数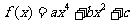 满足
满足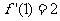 ,则
,则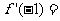
A.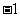 B.
B. C.2 D.0
C.2 D.0
3.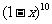 展开式中
展开式中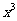 项的系数为
项的系数为
A.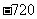 B.720 C.120 D.
B.720 C.120 D.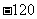
2.若集合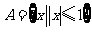 ,
,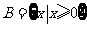 ,则
,则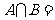
A.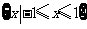 B.
B.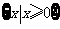
C.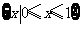 D.
D.
1.对于实数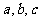 ,“
,“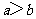 ”是“
”是“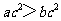 ”的
”的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
21、(本小题满分14分)
已知函数f(x)=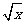 ,g(x)=alnx,a
,g(x)=alnx,a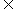 R。
R。
(1) 若曲线y=f(x)与曲线y=g(x)相交,且在交点处有相同的切线,求a的值及该切线的方程;
(2)
设函数h(x)=f(x)- g(x),当h(x)存在最小之时,求其最小值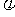 (a)的解析式;
(a)的解析式;
(3)
对(2)中的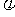 (a),证明:当a
(a),证明:当a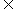 (0,+
(0,+ )时,
)时, 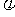 (a)
(a) 1.
1.
解 (1)f’(x)=
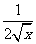 ,g’(x)=
,g’(x)=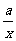 (x>0),
(x>0),
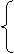 由已知得
由已知得 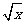 =alnx,
=alnx,
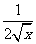 =
=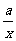 , 解德a=
, 解德a=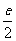 ,x=e2,
,x=e2,
 两条曲线交点的坐标为(e2,e) 切线的斜率为k=f’(e2)=
两条曲线交点的坐标为(e2,e) 切线的斜率为k=f’(e2)= 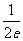 ,
,
 切线的方程为y-e=
切线的方程为y-e=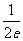 (x- e2).
(x- e2).
(1)
当a.>0时,令h  (x)=0,解得x=
(x)=0,解得x=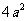 ,
,
所以当0 <
x< 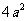 时 h
时 h  (x)<0,h(x)在(0,
(x)<0,h(x)在(0,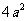 )上递减;
)上递减;
当x>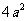 时,h
时,h  (x)>0,h(x)在(0,
(x)>0,h(x)在(0,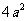 )上递增。
)上递增。
所以x>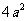 是h(x)在(0, +∞ )上的唯一极致点,且是极小值点,从而也是h(x)的最小值点。
是h(x)在(0, +∞ )上的唯一极致点,且是极小值点,从而也是h(x)的最小值点。
所以Φ (a)=h(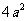 )= 2a-aln
)= 2a-aln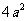 =2
=2
(2)当a ≤ 0时,h(x)=(1/2-2a) /2x>0,h(x)在(0,+∞)递增,无最小值。
故 h(x) 的最小值Φ (a)的解析式为2a(1-ln2a) (a>o)
(3)由(2)知Φ (a)=2a(1-ln2a)
则 Φ 1(a )=-2ln2a,令Φ 1(a )=0 解得 a =1/2
当 0<a<1/2时,Φ 1(a )>0,所以Φ (a ) 在(0,1/2) 上递增
当 a>1/2 时, Φ 1(a )<0,所以Φ(a ) 在 (1/2, +∞)上递减。
所以Φ(a )在(0, +∞)处取得极大值Φ(1/2 )=1
因为Φ(a )在(0, +∞)上有且只有一个极致点,所以Φ(1/2)=1也是Φ(a)的最大值
所当a属于 (0, +∞)时,总有Φ(a) ≤ 1
20.(本小题满分13分)
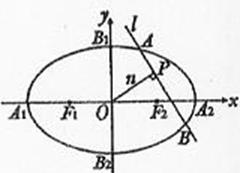 如图,椭圆C:
如图,椭圆C: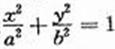 的顶点为A1,A2,B1,B2,焦点为F1,F2, | A1B1| =
的顶点为A1,A2,B1,B2,焦点为F1,F2, | A1B1| =
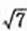 ,
,

(Ⅰ)求椭圆C的方程;
(Ⅱ)设n是过原点的直线,l是与n垂直相交于P点、与椭圆相交于A,B两点的直线,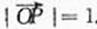 ,是否存在上述直线l使
,是否存在上述直线l使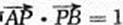 成立?若存在,求出直线l的方程;若不存在,请说明理由。
成立?若存在,求出直线l的方程;若不存在,请说明理由。
解 (1)由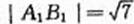 知a2+b2=7, ①
知a2+b2=7, ①
由 知a=2c,
②
知a=2c,
②
又b2=a2-c2 ③
由 ①②③解得a2=4,b2=3,
故椭圆C的方程为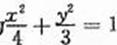 。
。
(2)设A,B两点的坐标分别为(x1,y1)(x2,y2)
假设使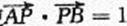 成立的直线l不存在,
成立的直线l不存在,
(1) 当l不垂直于x轴时,设l的方程为y=kx+m,
由l与n垂直相交于P点且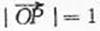 得
得
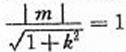 ,即m2=k2+1.
,即m2=k2+1.
∵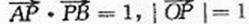 ,
,
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com