
题目列表(包括答案和解析)
(1) 已知集合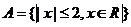 },
},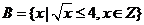 ,则
,则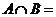
(A)(0,2) (B)[0,2] (C){0,2] (D){0,1,2}
(2)已知复数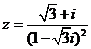 ,
,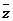 是z的共轭复数,则
是z的共轭复数,则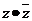 =
=
A. 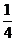 B.
B.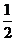 C.1
D.2
C.1
D.2
(3)曲线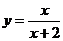 在点(-1,-1)处的切线方程为
在点(-1,-1)处的切线方程为
(A)y=2x+1 (B)y=2x-1 C y=-2x-3 D.y=-2x-2
(4)如图,质点P在半径为2的圆周上逆时针运动,其初始位置为P0(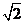 ,-
,-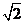 ),角速度为1,那么点P到x轴距离d关于时间t的函数图像大致为
),角速度为1,那么点P到x轴距离d关于时间t的函数图像大致为
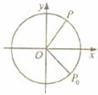
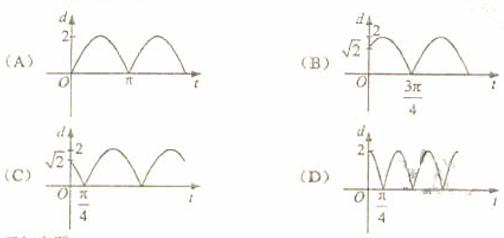
(5)已知命题
 :函数
:函数 在R为增函数,
在R为增函数,
 :函数
:函数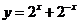 在R为减函数,
在R为减函数,
则在命题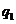 :
: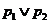 ,
,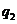 :
: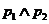 ,
,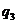 :
: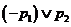 和
和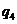 :
: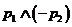 中,真命题是
中,真命题是
(A)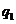 ,
,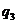 (B)
(B)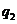 ,
,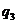 (C)
(C)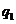 ,
,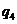 (D)
(D)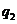 ,
,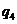
(6)某种种子每粒发芽的概率都为0.9,现播种了1000粒,对于没有发芽的种子,每粒需再补种2粒,补种的种子数记为X,则X的数学期望为
(A)100 (B)200 (C)300 (D)400
(7)如果执行右面的框图,输入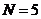 ,则输出的数等于
,则输出的数等于
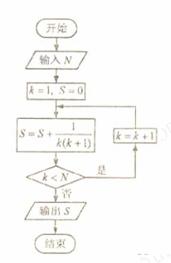
(A)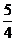
(B)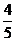
(C)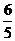
(D)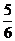
(8)设偶函数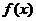 满足
满足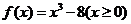 ,则
,则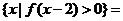
(A) 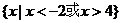 (B)
(B)
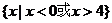
(C) 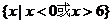 (D)
(D) 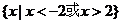
(9)若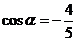 ,
,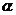 是第三象限的角,则
是第三象限的角,则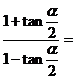
(A) 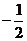 (B)
(B)
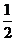 (C) 2 (D) -2
(C) 2 (D) -2
(10)设三棱柱的侧棱垂直于底面,所有棱长都为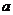 ,顶点都在一个球面上,则该球的表面积为
,顶点都在一个球面上,则该球的表面积为
(A) 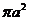 (B)
(B) 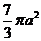 (C)
(C) 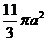 (D)
(D) 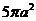
(11)已知函数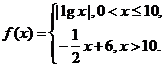 若
若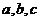 互不相等,且
互不相等,且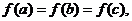 则
则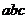 的取值范围是
的取值范围是
(A) 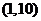 (B)
(B) 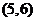 (C)
(C) 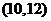 (D)
(D) 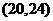
(12)已知双曲线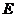 的中心为原点,
的中心为原点,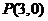 是
是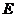 的焦点,过F的直线
的焦点,过F的直线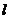 与
与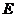 相交于A,B两点,且AB的中点为
相交于A,B两点,且AB的中点为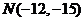 ,则
,则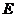 的方程式为
的方程式为
(A) 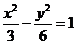 (B)
(B) 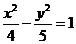 (C)
(C) 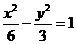 (D)
(D)
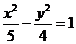
第Ⅱ卷
本卷包括必考题和选考题两部分,第(13)题~第(21)题为必考题,每个试题考生都必须做答,第(22)题~第(24)题为选考题,考试根据要求做答。
21. 本题设有(1)(2)(3)三个选考题,每题7分,请考生任选2题做答,满分14分。如果多做,则按所做的前两题计分。作答时,先用2B铅笔在答题卡上把所选题目对应的题号涂黑,并将所选题号填入括号中。
本题设有(1)(2)(3)三个选考题,每题7分,请考生任选2题做答,满分14分。如果多做,则按所做的前两题计分。作答时,先用2B铅笔在答题卡上把所选题目对应的题号涂黑,并将所选题号填入括号中。
(1)(本小题满分7分)选修4-2:矩阵与变换
已知矩阵M=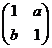 ,
,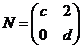 ,且
,且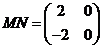 ,
,
(Ⅰ)求实数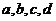 的值;(Ⅱ)求直线
的值;(Ⅱ)求直线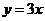 在矩阵M所对应的线性变换下的像的方程。
在矩阵M所对应的线性变换下的像的方程。
(2)(本小题满分7分)选修4-4:坐标系与参数方程
在直角坐标系xoy中,直线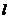 的参数方程为
的参数方程为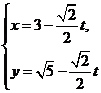 (t为参数)。在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为
(t为参数)。在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为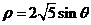 。
。
(Ⅰ)求圆C的直角坐标方程;(Ⅱ)设圆C与直线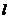 交于点A、B,若点P的坐标为
交于点A、B,若点P的坐标为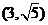 ,
,
求|PA|+|PB|。
(3)(本小题满分7分)选修4-5:不等式选讲
已知函数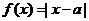 。K^S*5U.C#O%
。K^S*5U.C#O%
(Ⅰ)若不等式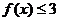 的解集为
的解集为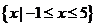 ,求实数
,求实数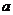 的值;
的值;
(Ⅱ)在(Ⅰ)的条件下,若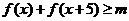 对一切实数x恒成立,求实数m的取值范围。
对一切实数x恒成立,求实数m的取值范围。
(1)选修4-2:矩阵与变换
[命题意图]本小题主要考查矩阵与变换等基础知识,考查运算求解能力。K^S*5U.C#O%
[解析](Ⅰ)由题设得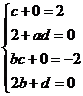 ,解得
,解得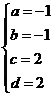 ;
;
(Ⅱ)因为矩阵M所对应的线性变换将直线变成直线(或点),所以可取直线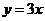 上的两(0,0),(1,3),
上的两(0,0),(1,3),
由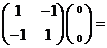
 ,
,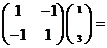
 得:点(0,0),(1,3)在矩阵M所对应的线性变换下的像是(0,0),(-2,2),从而
得:点(0,0),(1,3)在矩阵M所对应的线性变换下的像是(0,0),(-2,2),从而
直线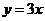 在矩阵M所对应的线性变换下的像的方程为
在矩阵M所对应的线性变换下的像的方程为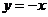 。
。
(2)选修4-4:坐标系与参数方程
[命题意图]本小题主要考查直线的参数方程、圆的极坐标方程、直线与圆的位置关系等基础知识,考查运算求解能力。
[解析](Ⅰ)由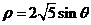 得
得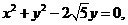 即
即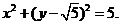
(Ⅱ)将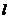 的参数方程代入圆C的直角坐标方程,得
的参数方程代入圆C的直角坐标方程,得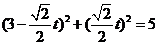 ,
,
即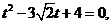 由于
由于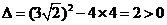 ,故可设
,故可设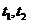 是上述方程的两实根,
是上述方程的两实根,
所以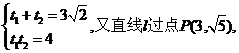 故由上式及t的几何意义得:
故由上式及t的几何意义得:
|PA|+|PB|=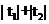 =
=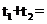
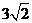 。
。
(3)选修4-5:不等式选讲
[命题意图]本小题主要考查绝对值的意义、绝对值不等式等基础知识,考查运算求解能力。
[解析](Ⅰ)由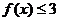 得
得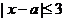 ,解得
,解得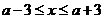 ,K^S*5U.C#O%
,K^S*5U.C#O%
又已知不等式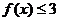 的解集为
的解集为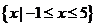 ,所以
,所以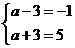 ,解得
,解得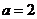 。
。
(Ⅱ)当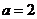 时,
时,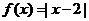 ,设
,设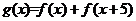 ,于是
,于是
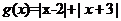 =
=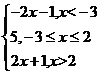 ,所以
,所以
当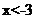 时,
时,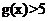 ;当
;当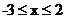 时,
时,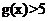 ;当
;当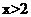 时,
时,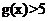 。
。
20.(本小题满分14分)
(Ⅰ)已知函数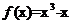 ,
,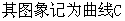 。
。
(i)求函数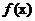 的单调区间;
的单调区间;
(ii)证明:若对于任意非零实数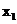 ,曲线C与其在点
,曲线C与其在点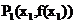 处的切线交于另一点
处的切线交于另一点
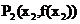 ,曲线C与其在点
,曲线C与其在点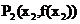 处的切线交于另一点
处的切线交于另一点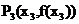 ,线段
,线段

(Ⅱ)对于一般的三次函数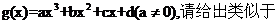 (Ⅰ)(ii)的正确命题,并予以证明。[.comZ*X*X*K]
(Ⅰ)(ii)的正确命题,并予以证明。[.comZ*X*X*K]
[命题意图]本小题主要考查函数、导数、定积分等基础知识,考查抽象概括能力、运算求解能力、推理论证能力,考查函数与方程思想、数形结合思想、化归与转化思想、特殊与一般思想。
[解析](Ⅰ)(i)由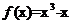 得
得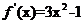 =
=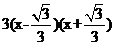 ,
,
当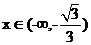 和
和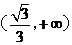 时,
时,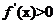 ;
;
当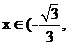
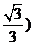 时,
时,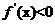 ,
,
因此,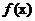 的单调递增区间为
的单调递增区间为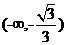 和
和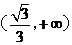 ,单调递减区间为
,单调递减区间为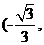
 。
。
19.(本小题满分13分)
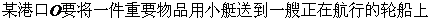 。
。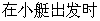 ,轮船位于港口O北偏西
,轮船位于港口O北偏西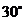 且与该港口相距20海里的A处,并以30海里/小时的航行速度沿正东方向匀速行驶。假设该小船沿直线方向以
且与该港口相距20海里的A处,并以30海里/小时的航行速度沿正东方向匀速行驶。假设该小船沿直线方向以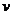 海里/小时的航行速度匀速行驶,经过t小时与轮船相遇。
海里/小时的航行速度匀速行驶,经过t小时与轮船相遇。
(1)若希望相遇时小艇的航行距离最小,则小艇航行速度的大小应为多少?
(2)假设小艇的最高航行速度只能达到30海里/小时,试设计航行方案(即确定航行方向与航行速度的大小),使得小艇能以最短时间与轮船相遇,并说明理由。
[解析]如图,由(1)得
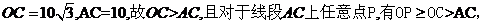 而小艇的最高航行速度只能达到30海里/小时,故轮船与小艇不可能在A、C(包含C)的任意位置相遇,设
而小艇的最高航行速度只能达到30海里/小时,故轮船与小艇不可能在A、C(包含C)的任意位置相遇,设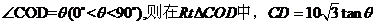 ,OD=
,OD=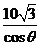 ,
,
由于从出发到相遇,轮船与小艇所需要的时间分别为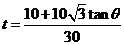 和
和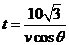 ,
,
所以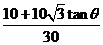
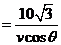 ,解得
,解得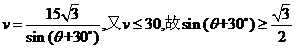 ,
,
从而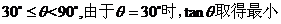 值,且最小值为
值,且最小值为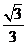 ,于是
,于是
当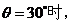
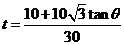 取得最小值,且最小值为
取得最小值,且最小值为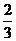 。
。
此时,在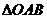 中,
中,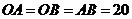 ,故可设计航行方案如下:
,故可设计航行方案如下:
航行方向为北偏东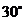 ,航行速度为30海里/小时,小艇能以最短时间与轮船相遇。
,航行速度为30海里/小时,小艇能以最短时间与轮船相遇。
17.(本小题满分13分)
已知中心在坐标原点O的椭圆C经过点A(2,3),且点F(2,0)为其右焦点。
(1)求椭圆C的方程;
(2)是否存在平行于OA的直线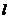 ,使得直线
,使得直线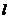 与椭圆C有公共点,且直线OA与
与椭圆C有公共点,且直线OA与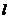 的距离等于4?若存在,求出直线
的距离等于4?若存在,求出直线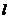 的方程;若不存在,请说明理由。
的方程;若不存在,请说明理由。
[命题意图]本小题主要考查直线、椭圆等基础知识,考查运算求解能力、推理论证能力,考查函数与方程思想、数形结合思想、化归与转化思想。
[解析](1)依题意,可设椭圆C的方程为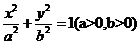 ,且可知左焦点为
,且可知左焦点为
 概率为
概率为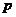 。
。
(i)当点C在圆周上运动时,求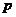 的最大值;
的最大值;
(ii)记平面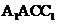 与平面
与平面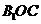 所成的角为
所成的角为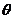
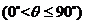 ,当
,当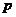 取最大值时,求
取最大值时,求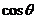 的值。
的值。
[命题意图]本小题主要考查直线与直线、直线与平面、平面与平面的位置关系,以及几何体的体积、几何概型等基础知识,考查空间想象能力、运算求解能力、推理论证能力,考查数形结合思想、化归与转化思想、必然与或然思想。
[解析](Ⅰ)因为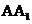
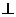 平面ABC,
平面ABC,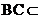 平面ABC,所以
平面ABC,所以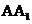
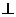
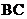 ,
,
因为AB是圆O直径,所以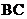
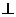
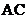 ,又
,又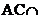
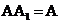 ,所以
,所以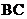
 平面
平面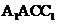 ,
,
而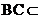 平面
平面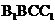 ,所以平面
,所以平面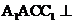 平面
平面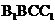 。K^S*5U.C#O%
。K^S*5U.C#O%
(Ⅱ)(i)设圆柱的底面半径为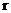 ,则AB=
,则AB=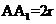 ,故三棱柱
,故三棱柱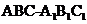 的体积为
的体积为
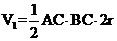 =
=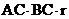 ,又因为
,又因为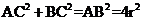 ,
,
所以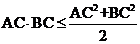 =
=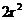 ,当且仅当
,当且仅当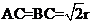 时等号成立,
时等号成立,
从而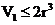 ,而圆柱的体积
,而圆柱的体积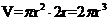 ,
,
故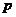 =
=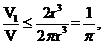 当且仅当
当且仅当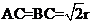 ,即
,即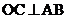 时等号成立,
时等号成立,
所以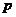 的最大值是
的最大值是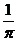 。K^S*5U.C#O%
。K^S*5U.C#O%
(ii)由(i)可知,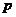 取最大值时,
取最大值时,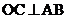 ,于是以O为坐标原点,建立空间直角坐标系
,于是以O为坐标原点,建立空间直角坐标系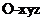 (如图),则C(r,0,0),B(0,r,0),
(如图),则C(r,0,0),B(0,r,0),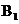 (0,r,2r),
(0,r,2r),
因为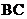
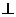 平面
平面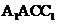 ,所以
,所以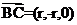 是平面
是平面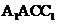 的一个法向量,
的一个法向量,
设平面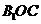 的法向量
的法向量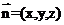 ,由
,由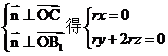 ,故
,故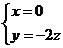 ,
,
取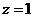 得平面
得平面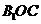 的一个法向量为
的一个法向量为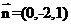 ,因为
,因为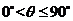 ,
,
所以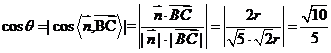 。
。
15.已知定义域为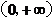 的函数
的函数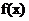 满足:①对任意
满足:①对任意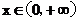 ,恒有
,恒有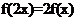 成立;当
成立;当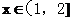 时,
时,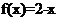 。给出如下结论:
。给出如下结论:
①对任意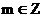 ,有
,有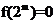 ;②函数
;②函数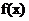 的值域为
的值域为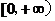 ;③存在
;③存在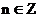 ,使得
,使得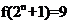 ;④“函数
;④“函数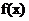 在区间
在区间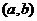 上单调递减”的充要条件是 “存在
上单调递减”的充要条件是 “存在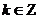 ,使得
,使得
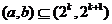 ”。
”。
其中所有正确结论的序号是 。
[答案]①②④
[解析]对①,因为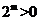 ,所以
,所以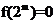 ,故①正确;经分析,容易得出②④也正确。
,故①正确;经分析,容易得出②④也正确。
[命题意图]本题考查函数的性质与充要条件,熟练基础知识是解答好本题的关键。

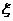 |
0 |
1 |
4 |
9 |
|
P |
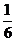 |
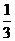 |
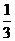 |
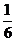 |
所以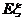 =
=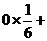
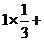
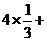

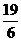 。
。
14.已知函数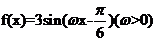 和
和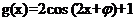 的图象的对称轴完全相同。若
的图象的对称轴完全相同。若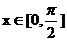 ,则
,则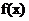 的取值范围是 。
的取值范围是 。
[答案]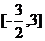
[解析]由题意知,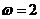 ,因为
,因为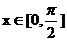 ,所以
,所以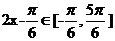 ,由三角函数图象知:
,由三角函数图象知:
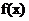 的最小值为
的最小值为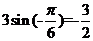 ,最大值为
,最大值为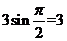 ,所以
,所以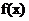 的取值范围是
的取值范围是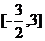 。
。
[命题意图]本题考查三角函数的图象与性质,考查了数形结合的数学思想。
13.某次知识竞赛规则如下:在主办方预设的5个问题中,选手若能连续正确回答出两个问题,即停止答题,晋级下一轮。假设某选手正确回答每个问题的概率都是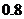 ,且每个问题的回答结果相互独立,则该选手恰好回答了4个问题就晋级下一轮的概率等于
。
,且每个问题的回答结果相互独立,则该选手恰好回答了4个问题就晋级下一轮的概率等于
。
[答案]0.128
[解析]由题意知,所求概率为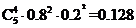 。
。
[命题意图]本题考查独立重复试验的概率,考查基础知识的同时,进一步考查同学们的分析问题、解决问题的能力。K^S*5U.C#O%
12.若一个底面是正三角形的三棱柱的正视图如图所示,则其表面积等于 .
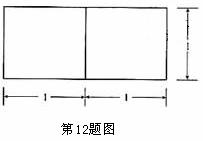
[答案]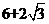
[解析]由正视图知:三棱柱是以底面边长为2,高为1的正三棱柱,所以底面积为
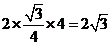 ,侧面积为
,侧面积为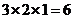 ,所以其表面积为
,所以其表面积为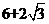 。K^S*5U.C#O%
。K^S*5U.C#O%
[命题意图]本题考查立体几何中的三视图,考查同学们识图的能力、空间想象能力等基本能力。
11.在等比数列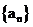 中,若公比
中,若公比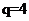 ,且前3项之和等于21,则该数列的通项公式
,且前3项之和等于21,则该数列的通项公式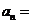 .
.
[答案]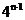
[解析]由题意知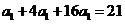 ,解得
,解得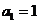 ,所以通项
,所以通项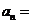
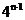 。
。
[命题意图]本题考查等比数列的通项公式与前n项和公式的应用,属基础题。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com