
题目列表(包括答案和解析)
20.(本题满分14分)
设函数

(1)当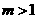 时,求函数
时,求函数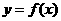 在
在 上的最大值;
上的最大值;
(2)记函数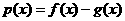 ,若函数
,若函数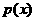 有零点,求
有零点,求 的取值范围.
的取值范围.
19.解:(1)当点P不在x轴上时,延长F1M与F2P的延长线相交于点N,连结OM,
∵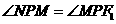 ,
,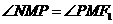 ∴
∴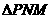 ≌
≌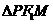 ∴M是线段
∴M是线段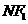 的中点,
的中点,

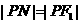 |----------------------------------------------------2分
|----------------------------------------------------2分
∴  =
=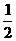
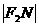 =
=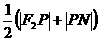 =
=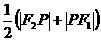
∵点P在椭圆上
∴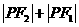 =
=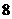 ∴
∴ =4,----------------------4分
=4,----------------------4分
当点P在x轴上时,M与P重合
 ∴M点的轨迹T的方程为:
∴M点的轨迹T的方程为: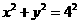 .----------------------6分
.----------------------6分
(2)连结OE,易知轨迹T上有两个点
A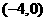 ,B
,B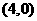 满足
满足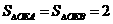 ,
,
分别过A、B作直线OE的两条平行线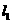 、
、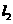 .
.
∵同底等高的两个三角形的面积相等
∴符合条件的点均在直线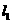 、
、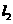 上.------------------------------------7分
上.------------------------------------7分
∵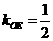 ∴直线
∴直线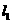 、
、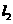 的方程分别为:
的方程分别为: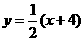 、
、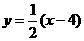 -------------------8分
-------------------8分
设点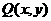 (
(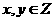 )∵
)∵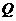 在轨迹T内,∴
在轨迹T内,∴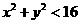 --------------------------------9分
--------------------------------9分
分别解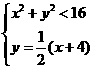 与
与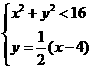
得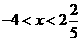 与
与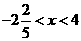 --------------------------------------------------------------------11分
--------------------------------------------------------------------11分
∵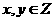 ∴
∴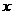 为偶数,在
为偶数,在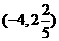 上
上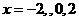 对应的
对应的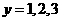
在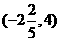 上
上 ,对应的
,对应的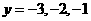 ------------------------------------------------13分
------------------------------------------------13分
∴满足条件的点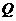 存在,共有6个,它们的坐标分别为:
存在,共有6个,它们的坐标分别为:
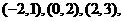
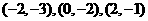 .-----------------------------------------------------14分
.-----------------------------------------------------14分
19.(本题满分14分)
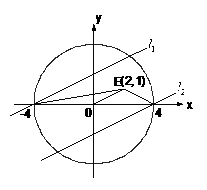
已知如图,椭圆方程为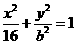
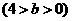 .P为椭圆上的动点,
.P为椭圆上的动点,
F1、F2为椭圆的两焦点,当点P不在x轴上时,过F1作∠F1PF2的外角
平分线的垂线F1M,垂足为M,当点P在x轴上时,定义M与P重合.
(1)求M点的轨迹T的方程;
(2)已知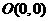 、
、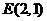 ,试探究是否存在这样的点
,试探究是否存在这样的点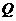 :
: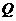 是轨迹T内部的整点(平面内横、纵坐标均为整数的点称为整点),且△OEQ的面积
是轨迹T内部的整点(平面内横、纵坐标均为整数的点称为整点),且△OEQ的面积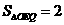 ?若存在,求出点Q的坐标,若不存在,说明理由.
?若存在,求出点Q的坐标,若不存在,说明理由.
24.(本题满分10分)
证明:下面用数学归纳法证明
(1)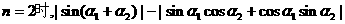
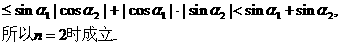
(2)假设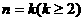 时成立,即
时成立,即


由(1)(2)得,原式成立。 ………………10分
23.(本题满分10分)
(I)直线的普通方程为: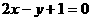 ;
;
圆的直角坐标方程为: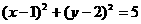 ………………4分
………………4分
(II)圆心到直线的距离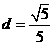 ,
,
直线被圆截得的弦长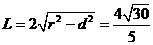 ………………10分
………………10分
22.(本题满分10分)
(I)证明:

∴圆心O在直线AD上。 ………………5分
(II)连接DF,由(I)知,DH是⊙O的直径,

∴点C是线段GD的中点。 ………………10分
22.(本小题满分10分)选修4-1:几何证明选讲
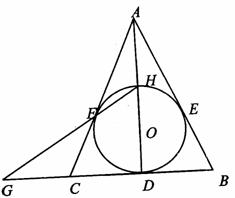 如图,⊙O内切于△ABC的边于D,E,F,AB=AC,连接AD交⊙O于点H,直线HF交BC的延长线于点G。
如图,⊙O内切于△ABC的边于D,E,F,AB=AC,连接AD交⊙O于点H,直线HF交BC的延长线于点G。
(I)求证:圆心O在直线AD上;
(II)求证:点C是线段GD的中点。
21.(本题满分12分)
解:(I)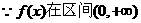 上是单调增函数,
上是单调增函数,
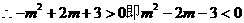
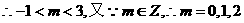 ………………2分
………………2分
而 是偶函数。
是偶函数。
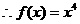 ………………4分
………………4分
(II)(i)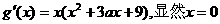 不是方程
不是方程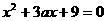 的根。
的根。
为使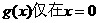 处有极值,
处有极值,
必须 恒成立, ………………6分
恒成立, ………………6分
即有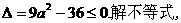
得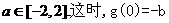 是唯一极值。
是唯一极值。
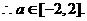 ………………8分
………………8分
(ii)由条件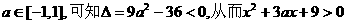 恒成立。
恒成立。
当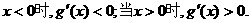 ………………9分
………………9分
因此函数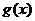 在[-2,2]上的最大值是
在[-2,2]上的最大值是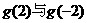 两者中较大者。 …………10分
两者中较大者。 …………10分
为使对方任意的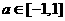 ,不等式
,不等式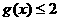 在[-2,2]上恒成立,
在[-2,2]上恒成立,
当且仅当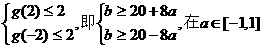 上恒成立。
上恒成立。
所以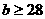 ,因此满足条件的b的取值范围是
,因此满足条件的b的取值范围是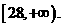 …………12分
…………12分
请考生在第22、23、24三题中任选一题作答,如果多做,则按所做的第一题记分。
21.(本小题满分12分)
已知幂函数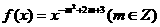 为偶函数,且在区间
为偶函数,且在区间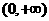 上是单调增函数。
上是单调增函数。
(I)求函数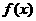 的解析式;
的解析式;
(II)设函数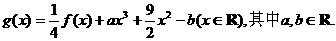
(i)若函数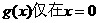 处有极值,求a的取值范围;
处有极值,求a的取值范围;
(ii)对于任意的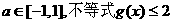 在[-2,2]上恒成立,求
在[-2,2]上恒成立,求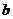 的取值范围。
的取值范围。
20.(本题满分12分)
(I)由
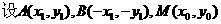
由A,M是椭圆上的点得,
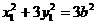 ①
①
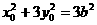 ②
②
①-②得,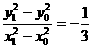
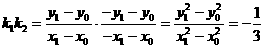 (定值) ………………5分
(定值) ………………5分
(II)点M的坐标为(0,1),则
显然直线AB的斜率存在,设直线AB的方程为 ,代入椭圆方程得,
,代入椭圆方程得,
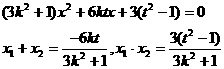
由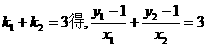 ③,
③,
又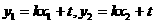 ④,
④,
由③,④得, ,
,
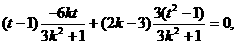
化简得,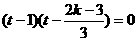
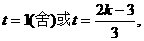 ………………9分
………………9分
则直线AB的方程为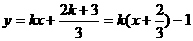
 ………………10分
………………10分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com