
题目列表(包括答案和解析)
20. (本小题满分16分)数列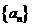 中,
中,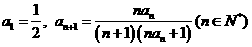 ,其前
,其前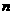 项的和为
项的和为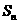 .求证:
.求证: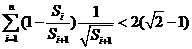 .
.
19.解: 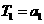 ,对
,对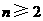 反复使用上述关系式,得
反复使用上述关系式,得
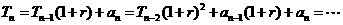
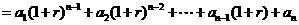 , ①
, ①
在①式两端同乘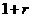 ,得
,得
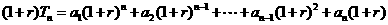 ②
②
②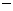 ①,得
①,得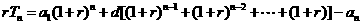
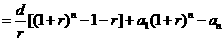 .
.
即 .
.
如果记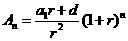 ,
,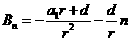 ,
,
则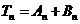 .
.
其中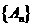 是以
是以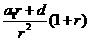 为首项,以
为首项,以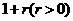 为公比的等比数列;
为公比的等比数列;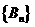 是以
是以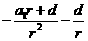 为首项,
为首项,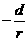 为公差的等差数列.
为公差的等差数列.
19.(本小题满分16分)
公民在就业的第一年就交纳养老储备金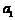 ,以后每年交纳的数目均比上一年增加
,以后每年交纳的数目均比上一年增加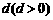 ,历年所交纳的储备金数目
,历年所交纳的储备金数目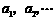 是一个公差为
是一个公差为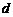 的等差数列.与此同时,国家给予优惠的计息政策,不仅采用固定利率,而且计算复利.如果固定年利率为
的等差数列.与此同时,国家给予优惠的计息政策,不仅采用固定利率,而且计算复利.如果固定年利率为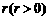 ,那么,在第
,那么,在第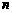 年末,第一年所交纳的储备金就变为
年末,第一年所交纳的储备金就变为 ,第二年所交纳的储备金就变为
,第二年所交纳的储备金就变为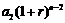 ,
, .以
.以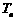 表示到第
表示到第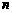 年末所累计的储备金总额.
年末所累计的储备金总额.
求证: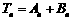 ,其中
,其中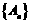 是一个等比数列,
是一个等比数列,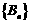 是一个等差数列.
是一个等差数列.
18.解:(I)证明:首先,由 中元素构成的有序数对
中元素构成的有序数对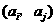 共有
共有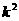 个.
个.
因为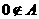 ,所以
,所以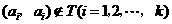 ;
;
又因为当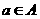 时,
时,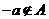 时,
时,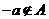 ,所以当
,所以当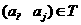 时,
时,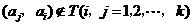 .
.
从而,集合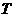 中元素的个数最多为
中元素的个数最多为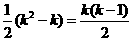 ,
,
即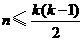 .
.
(II)解: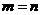 ,证明如下:
,证明如下:
(1)对于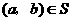 ,根据定义,
,根据定义,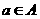 ,
, ,且
,且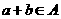 ,从而
,从而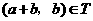 .
.
如果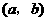 与
与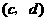 是
是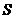 的不同元素,那么
的不同元素,那么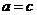 与
与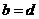 中至少有一个不成立,从而
中至少有一个不成立,从而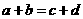 与
与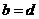 中也至少有一个不成立.
中也至少有一个不成立.
故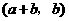 与
与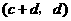 也是
也是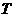 的不同元素.
的不同元素.
可见,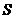 中元素的个数不多于
中元素的个数不多于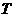 中元素的个数,即
中元素的个数,即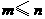 ,
,
(2)对于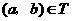 ,根据定义,
,根据定义,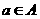 ,
, ,且
,且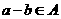 ,从而
,从而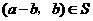 .如果
.如果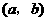 与
与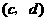 是
是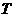 的不同元素,那么
的不同元素,那么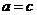 与
与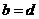 中至少有一个不成立,从而
中至少有一个不成立,从而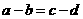 与
与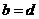 中也不至少有一个不成立,
中也不至少有一个不成立,
故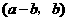 与
与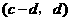 也是
也是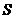 的不同元素.
的不同元素.
可见,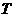 中元素的个数不多于
中元素的个数不多于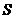 中元素的个数,即
中元素的个数,即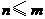 ,
,
由(1)(2)可知,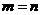 .
.
18. (本小题满分14分)
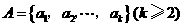 ,其中
,其中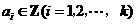 ,由
,由 中的元素构成两个相应的集合:
中的元素构成两个相应的集合: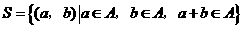 ,
,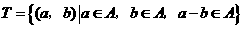 .其中
.其中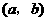 是有序数对,集合
是有序数对,集合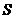 和
和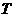 中的元素个数分别为
中的元素个数分别为 和
和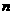 .若对于任意的
.若对于任意的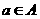 ,总有
,总有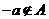 ,则称集合
,则称集合 具有性质
具有性质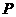 .
.
(I)对任何具有性质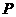 的集合
的集合 ,证明:
,证明: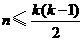 ;
;
(II)判断 和
和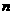 的大小关系,并证明你的结论.
的大小关系,并证明你的结论.
17. 解:(Ⅰ)∵ ,
,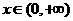
∴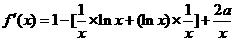 ,
,
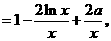 ……2分
……2分
∴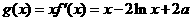 ,
,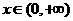
∴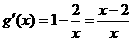 ,令
,令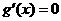 ,得
,得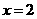 ,
……4分
,
……4分
列表如下:
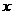 |
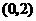 |
2 |
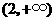 |
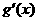 |
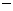 |
0 |
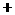 |
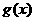 |
 |
极小值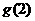 |
 |
∴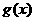 在
在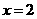 处取得极小值
处取得极小值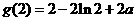 ,
,
即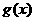 的最小值为
的最小值为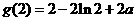 .
……6分
.
……6分
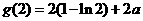 ,
,
∵ ,∴
,∴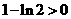 ,又
,又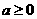 ,
,
∴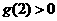 .
……8分
.
……8分
证明(Ⅱ)由(Ⅰ)知,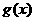 的最小值是正数,
的最小值是正数,
∴对一切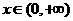 ,恒有
,恒有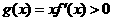 ,
……10分
,
……10分
从而当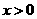 时,恒有
时,恒有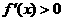 ,
……11分
,
……11分
故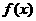 在
在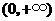 上是增函数.
……12分
上是增函数.
……12分
证明(Ⅲ)由(Ⅱ)知: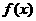 在
在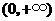 上是增函数,
上是增函数,
∴当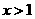 时,
时,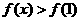 ,
……13分
,
……13分
又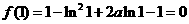 ,
……14分
,
……14分
∴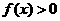 ,即
,即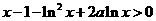 ,
……15分
,
……15分
∴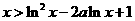
故当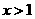 时,恒有
时,恒有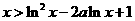 .
……16分
.
……16分
17. (本小题满分15分)设常数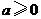 ,函数
,函数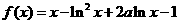
(1)令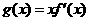
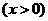 ,求
,求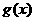 的最小值,并比较
的最小值,并比较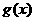 的最小值与0的大小;
的最小值与0的大小;
(2)求证: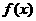 在
在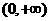 上是增函数;
上是增函数;
(3)求证:当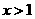 时,恒有
时,恒有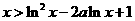 .
.
21.解:(1)解方程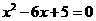 得
得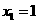 ,
,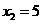 ,---------------------------------------------1分
,---------------------------------------------1分
∴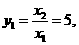 ---------------------------------------------------------------------------------------------2分
---------------------------------------------------------------------------------------------2分
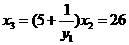 ,
,
∴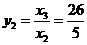 ,------------------------------------------------------------------------------------------3分
,------------------------------------------------------------------------------------------3分
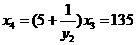 ,∴
,∴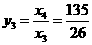 ---------------------------------------------------------4分
---------------------------------------------------------4分
(2)由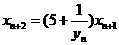 得
得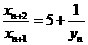
即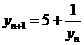
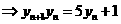 ----------------------------------------------------------------6分
----------------------------------------------------------------6分
当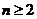 时
时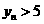 ,于是
,于是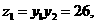
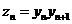 =
=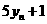
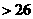 (
(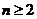 )
)
∴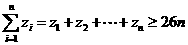 --------------------------------------------------------------------9分
--------------------------------------------------------------------9分
(3)当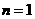 时
时
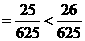 ,结论成立;------------------------------------------10分
,结论成立;------------------------------------------10分
当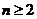 时,有
时,有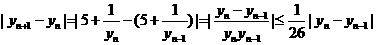
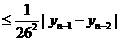
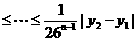 =
=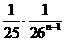 ----------------------------------------12分
----------------------------------------12分
∵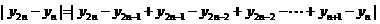
∴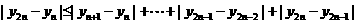
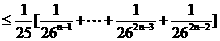
=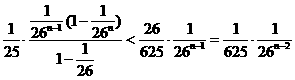
∴对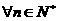 有
有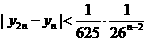
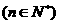 ----------------------------------------------14分
----------------------------------------------14分
21.(本题满分14分)
|
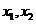 (
(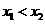 )是方程
)是方程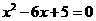 的两根,且
的两根,且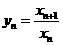 ,
,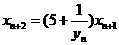 .
.
(1)求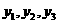 的值;
的值;
(2)设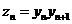 ,求证:
,求证: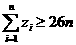 ;
;
(3)求证:对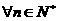 有
有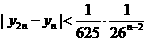 w。.w..
w。.w..
20.解:(1)当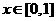 时,
时,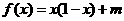 =
=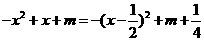
∴当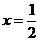 时,
时,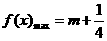 -----------------------------------------------------------------2分
-----------------------------------------------------------------2分
当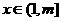 时,
时,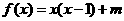 =
=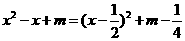
∵函数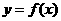 在
在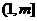 上单调递增 ∴
上单调递增 ∴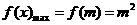 ------------------------------4分
------------------------------4分
由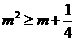 得
得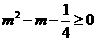 又
又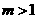
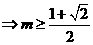
∴当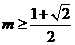 时,
时,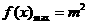 ,当
,当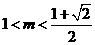 时,
时,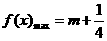 .----------6分
.----------6分
(2)函数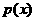 有零点即方程
有零点即方程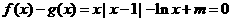 有解
有解
即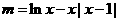 有解-------------------------------------------------------------------------------7分
有解-------------------------------------------------------------------------------7分
令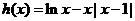
当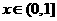 时
时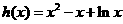
∵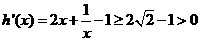 --------------------------------------------------------------------9分
--------------------------------------------------------------------9分
∴函数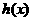 在
在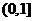 上是增函数,∴
上是增函数,∴ ---------------------------------------------10分
---------------------------------------------10分
当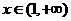 时,
时,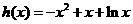
∵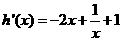
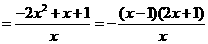
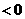 --------------------------------12分
--------------------------------12分
∴函数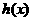 在
在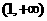 上是减函数,∴
上是减函数,∴ -----------------------------------------13分
-----------------------------------------13分
∴方程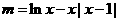 有解时
有解时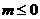
即函数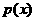 有零点时
有零点时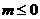 ---------------------------------------------------------------------------14分
---------------------------------------------------------------------------14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com