
题目列表(包括答案和解析)
21.(1)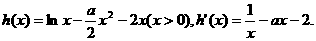
若使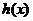 存在单调递减区间,则
存在单调递减区间,则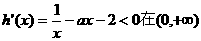 上有解.……1分
上有解.……1分
而当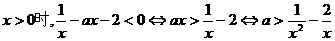
问题转化为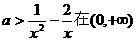 上有解,故a大于函数
上有解,故a大于函数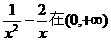 上的最小值.
上的最小值.
………………3分
又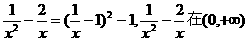 上的最小值为-1,所以a>1.……4分
上的最小值为-1,所以a>1.……4分
(2)令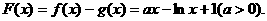
函数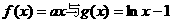 的交点个数即为函数
的交点个数即为函数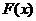 的零点的个数.……5分
的零点的个数.……5分
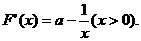
令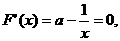 解得
解得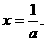
随着x的变化,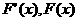 的变化情况如下表:
的变化情况如下表:
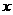 |
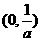 |
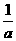 |
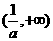 |
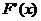 |
- |
0 |
+ |
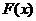 |
单调递减 |
极(最)小值2+lna |
单调递增 |
…………7分
①当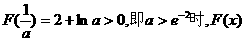 恒大于0,函数
恒大于0,函数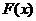 无零点.……8分
无零点.……8分
②当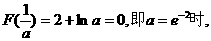 由上表,函数
由上表,函数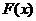 有且仅有一个零点.
有且仅有一个零点.
……9分
③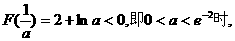 显然
显然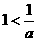
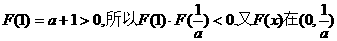 内单调递减,
内单调递减,
所以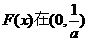 内有且仅有一个零点 …………10分
内有且仅有一个零点 …………10分
当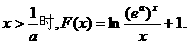
由指数函数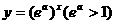 与幂函数
与幂函数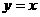 增长速度的快慢,知存在
增长速度的快慢,知存在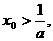
使得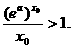
从而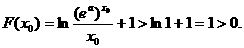
因而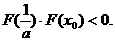
又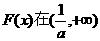 内单调递增,
内单调递增,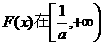 上的图象是连续不断的曲线,
上的图象是连续不断的曲线,
所以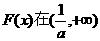 内有且仅有一个零点. …………11分
内有且仅有一个零点. …………11分
因此,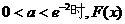 有且仅有两个零点.
有且仅有两个零点.
综上,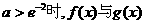 的图象无交点;当
的图象无交点;当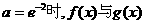 的图象有且仅有一个交点;
的图象有且仅有一个交点;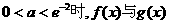 的图像有且仅有两个交点.……12分
的图像有且仅有两个交点.……12分
21.(本题满分12分)
已知函数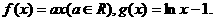
(1)若函数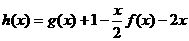 存在单调递减区间,求a的取值范围;
存在单调递减区间,求a的取值范围;
(2)当a>0时,试讨论这两个函数图象的交点个数.
20.(1)当n=1时,有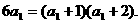
解得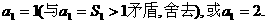 …………1分
…………1分
当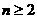 时,有
时,有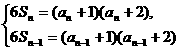 两式相减得
两式相减得
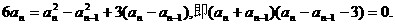 …………3分
…………3分
由题设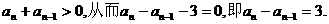
故数列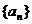 是首项为2,公差为3的等差数列
是首项为2,公差为3的等差数列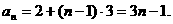 ……5分
……5分
(2)由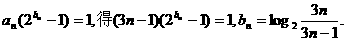 …………6分
…………6分
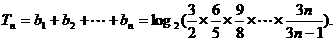
而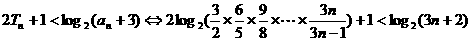
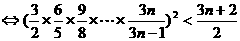
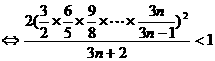 …………8分
…………8分
令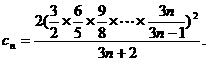
则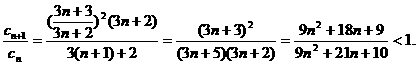
而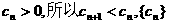 是单调递减数列.…………10分
是单调递减数列.…………10分
所以,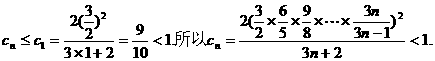
从而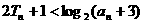 成立. …………12分
成立. …………12分
20.(本小题满分12分)
已知各项均为正数的数列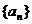 的前n项和
的前n项和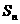 满足
满足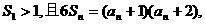
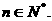
(1)求数列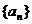 的通项公式;
的通项公式;
(2)设数列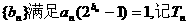 为数列
为数列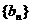 的前n项和,求证:
的前n项和,求证:
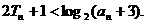
22.解:(1)设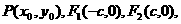
则由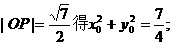
由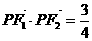 得
得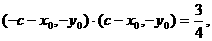
即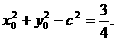
所以c=1 …………2分
又因为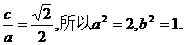 …………3分
…………3分
因此所求椭圆的方程为: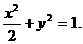 …………4分
…………4分
(2)动直线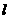 的方程为:
的方程为: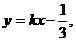
由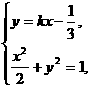 得
得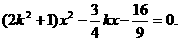
设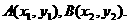
则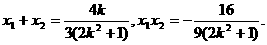 …………6分
…………6分
假设在y上存在定点M(0,m),满足题设,则
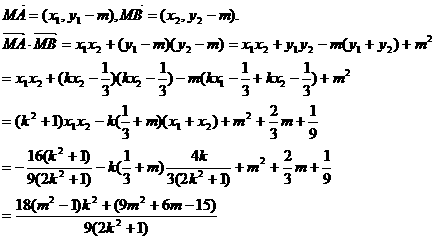
由假设得对于任意的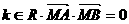 恒成立,
恒成立,
即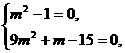 解得m=1。
解得m=1。
因此,在y轴上存在定点M,使得以AB为直径的圆恒过这个点,
点M的坐标为(0,1) …………10分
这时,点M到AB的距离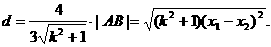
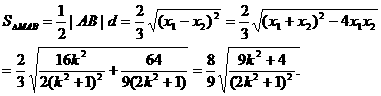
设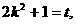 则
则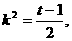
得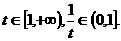
所以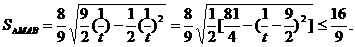
当且仅当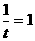 时,上式等号成立。
时,上式等号成立。
因此, 面积的最大值是
面积的最大值是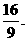 …………14分
…………14分
22.(本小题满分14分)
已知椭圆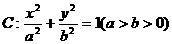 的离心率为
的离心率为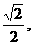 其左、右焦点分别为
其左、右焦点分别为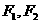 ,点P是坐标平面内一点,且
,点P是坐标平面内一点,且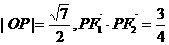 (O为坐标原点)。
(O为坐标原点)。
(1)求椭圆C的方程;
(2)过点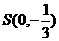 且斜率为k的动直线
且斜率为k的动直线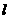 交椭圆于A、B两点,在y轴上是否存在定点M,使以AB为直径的圆恒过这个点?若存在,求出M的坐标和
交椭圆于A、B两点,在y轴上是否存在定点M,使以AB为直径的圆恒过这个点?若存在,求出M的坐标和 面积的最大值;若不存在,说明理由。
面积的最大值;若不存在,说明理由。
21.解:(1)由题意知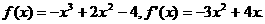
令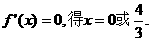
当x在[-1,1]上变化时,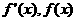 随x的变化情况如下表:
随x的变化情况如下表:
|
x |
-1 |
(-1,0) |
0 |
(0,1) |
1 |
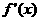 |
-7 |
- |
0 |
+ |
1 |
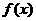 |
-1 |
↓ |
-4 |
↑ |
-3 |
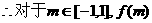 的最小值为
的最小值为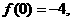
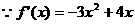 的对称轴为
的对称轴为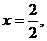 且抛物线开口向下
且抛物线开口向下
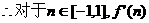 的最小值为
的最小值为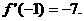
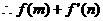 的最小值为-11。 …………6分
的最小值为-11。 …………6分
(2)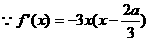
①若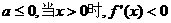
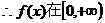 上单调递减,
上单调递减,
又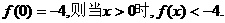
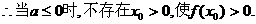
②若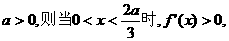
当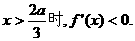
从而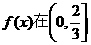 上单调递增,在
上单调递增,在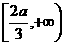 上单调递减,
上单调递减,
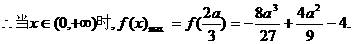
根据题意,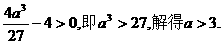
综上,a的取值范围是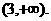 …………12分
…………12分
21.(本小题满分12分)
已知函数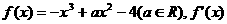 是
是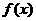 的导函数。
的导函数。
(1)当a=2时,对于任意的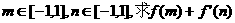 的最小值;
的最小值;
(2)若存在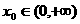 ,使
,使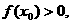 求a的取值范围。
求a的取值范围。
20.解:(1)由已知得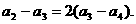
从而得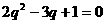
解得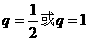 (舍去) …………4分
(舍去) …………4分
所以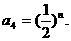 …………6分
…………6分
(2)由于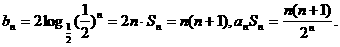
因此所证不等式等价于: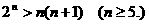
①当n=5时,因为左边=32,右边=30,所以不等式成立;
②假设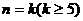 时不等式成立,即
时不等式成立,即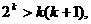
两边同乘以2得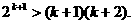
这说明当n=k+1时也不等式成立。
由①②知,当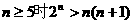 成立。
成立。
因此,当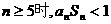 成立。 …………12分
成立。 …………12分
20.(本小题满分12分)
已知等比数列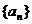 中,
中,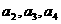 分别是某等差数列的第5项、第3项、第2项,且
分别是某等差数列的第5项、第3项、第2项,且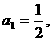 公比
公比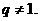
(1)求数列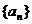 的通项公式;
的通项公式;
(2)已知数列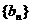 满足
满足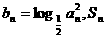 是数列
是数列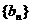 的前n项和,
的前n项和,
求证:当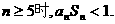
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com