
题目列表(包括答案和解析)
4、已知P是△ABC所在平面内的一点,若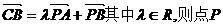 一定在( )
一定在( )
A.△ABC的内部 B.AC边所在的直线上
C.AB边所在直线上 D.BC边所在的直线上
3、若圆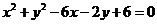 上有且仅有三个点到直线
上有且仅有三个点到直线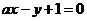 (a是实数)的距离为1,则a等于( ). A.
(a是实数)的距离为1,则a等于( ). A.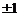 B.
B.
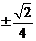 C.
C. 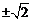 D.
D. 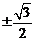
2、已知|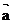 |=3,|
|=3,|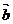 |=1,且
|=1,且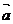 与
与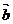 同向共线,则
同向共线,则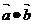 是 ( )
是 ( )
A.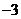 B.0
C.3
D.–3或3
B.0
C.3
D.–3或3
1、已知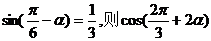 的值是( )A.
的值是( )A.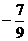 B.
B.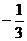 C.
C.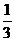 D.
D.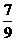
22.(1)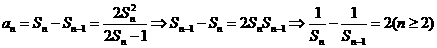
所以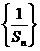 是等差数列。则
是等差数列。则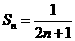 。
。
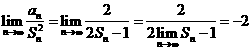 。
。
(2)当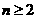 时,
时,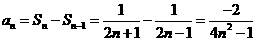 ,
,
综上,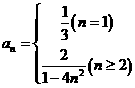 。
。
(3)令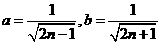 ,当
,当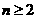 时,有
时,有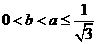 (1)
(1)
法1:等价于求证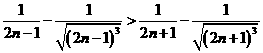 。
。
当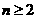 时,
时,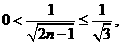 令
令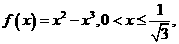
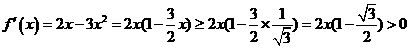 ,
,
则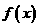 在
在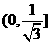 递增。
递增。
又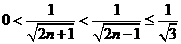 ,
,
所以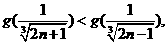 即
即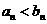 。
。
法(2)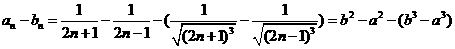
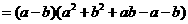 (2)
(2)
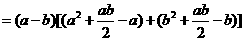
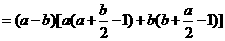 (3)
(3)
因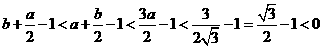
所以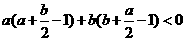
由(1)(3)(4)知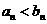 。
。
法3:令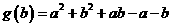 ,则
,则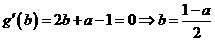
所以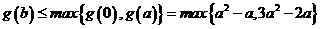
因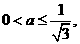 则
则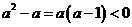
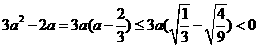
所以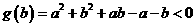 (5)
(5)
由(1)(2)(5)知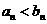
22.(14分)已知数列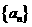 中,
中,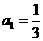 ,当
,当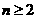 时,其前
时,其前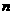 项和
项和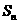 满足
满足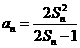 ,
,
(2)
求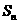 的表达式及
的表达式及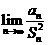 的值;
的值;
(3)
求数列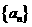 的通项公式;
的通项公式;
(4)
设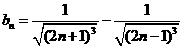 ,求证:当
,求证:当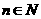 且
且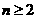 时,
时,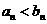 。
。
21.(1)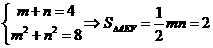
(2)
因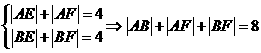 ,
,
则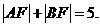
(1)
设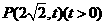
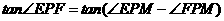
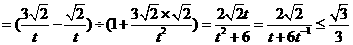 ,
,
当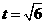 时,
时,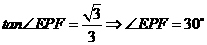
21.(12分)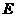 、
、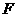 是椭圆
是椭圆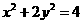 的左、右焦点,
的左、右焦点,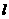 是椭圆的右准线,点
是椭圆的右准线,点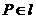 ,过点
,过点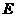 的直线交椭圆于
的直线交椭圆于 、
、 两点。
两点。
(1)
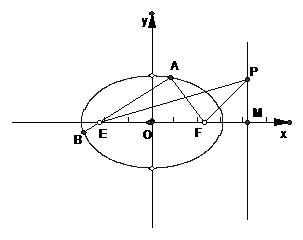 当
当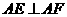 时,求
时,求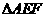 的面积;
的面积;
(2)
当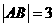 时,求
时,求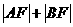 的大小;
的大小;
(3)
求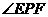 的最大值。
的最大值。
22.(本小题满分14分)
解: (1)设点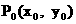 是函数
是函数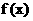 的图象上任意一点, 其关于点
的图象上任意一点, 其关于点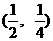 的对称点为
的对称点为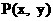 .
.
由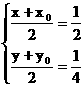 得
得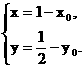
所以, 点P的坐标为P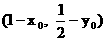 .………………(2分)
.………………(2分)
由点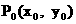 在函数
在函数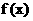 的图象上, 得
的图象上, 得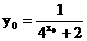 .
.
∵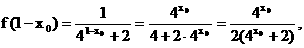
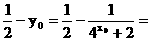
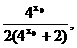 ∴点P
∴点P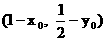 在函数
在函数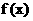 的图象上.
的图象上.
∴函数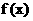 的图象关于点
的图象关于点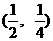 对称. ………………(4分)
对称. ………………(4分)
(2)由(1)可知, 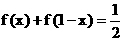 , 所以
, 所以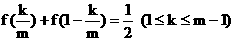 ,
,
即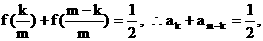 ………………(6分)
………………(6分)
由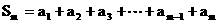 , ……………… ①
, ……………… ①
得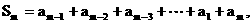 ………………②
………………②
由①+②, 得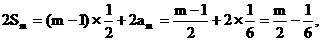
∴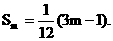 ………………(8分)
………………(8分)
(3) ∵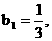
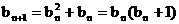 , ………………③
, ………………③
∴对任意的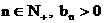 . ………………④
. ………………④
由③、④, 得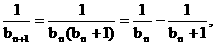 即
即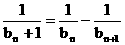 .
.
∴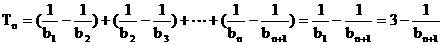 .……………(10分)
.……………(10分)
∵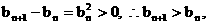 ∴数列
∴数列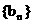 是单调递增数列.
是单调递增数列.
∴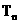 关于n递增. 当
关于n递增. 当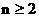 , 且
, 且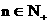 时,
时, 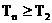 .
.
∵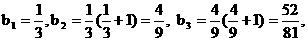
∴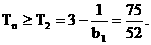 ………………(12分)
………………(12分)
∴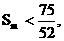 即
即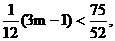 ∴
∴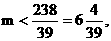 ∴m的最大值为6. ……………(14分)
∴m的最大值为6. ……………(14分)
22.(本小题满分14分)已知函数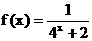
 .
.
(1) 试证函数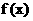 的图象关于点
的图象关于点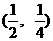 对称;
对称;
(2) 若数列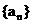 的通项公式为
的通项公式为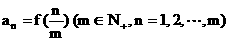 , 求数列
, 求数列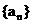 的前m项和
的前m项和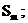
(3) 设数列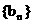 满足:
满足: 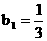 ,
, 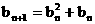 .
.
设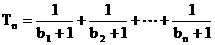 .
.
若(2)中的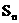 满足对任意不小于2的正整数n,
满足对任意不小于2的正整数n, 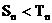 恒成立, 试求m的最大值.
恒成立, 试求m的最大值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com