
题目列表(包括答案和解析)
20.解:(Ⅰ)由题意知椭圆的焦点在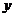 轴上,设椭圆方程为
轴上,设椭圆方程为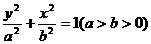 ,
,
由题意知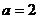 ,
,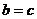 ,又
,又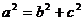 则
则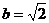 ,
,
所以椭圆方程为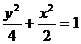 --------------------------------------4分
--------------------------------------4分
(Ⅱ)设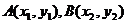 ,由题意,直线
,由题意,直线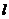 的斜率存在,
的斜率存在,
设其方程为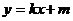 ,与椭圆方程联立
,与椭圆方程联立
即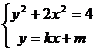 ,
,
则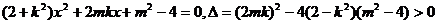
由韦达定理知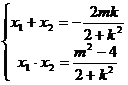 ;----------------------------------------6分
;----------------------------------------6分
又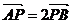 ,即有
,即有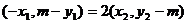
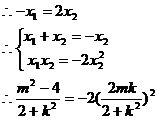 --------------------------------------------8分
--------------------------------------------8分
整理得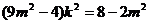
又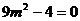 时不成立,所以
时不成立,所以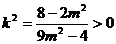 ---------------------------10分
---------------------------10分
得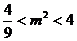 ,此时
,此时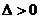
所以m的取值范围为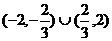 .-------------------------------------12分
.-------------------------------------12分
20. 已知椭圆C的中心为坐标原点O,一个长轴端点为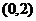 ,短轴端点和焦点所组成的四边形为正方形,直线
,短轴端点和焦点所组成的四边形为正方形,直线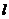 与y轴交于点
与y轴交于点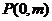 ,与椭圆C交于相异两点A、B,且
,与椭圆C交于相异两点A、B,且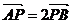 .
.
(Ⅰ)求椭圆方程;
(Ⅱ)求m的取值范围.
21.(本小题满分14分)
解:(1)令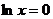 ,得
,得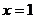 ,且
,且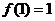 ,
,
所以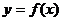 的图象过定点
的图象过定点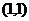 ; ……………………………………………2分
; ……………………………………………2分
(2)当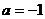 时,
时,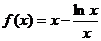 ,
,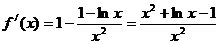 ………4分
………4分
令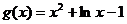 ,经观察得
,经观察得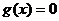 有根
有根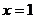 ,下证明
,下证明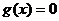 无其它根.
无其它根.
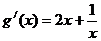 ,当
,当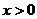 时,
时,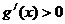 ,即
,即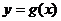 在
在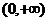 上是单调递增函数.
上是单调递增函数.
所以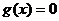 有唯一根
有唯一根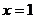 ;且当
;且当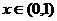 时,
时,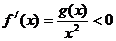 ,
,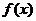 在
在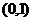 上是减函数;当
上是减函数;当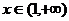 时,
时,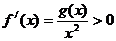 ,
,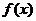 在
在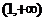 上是增函数;
上是增函数;
…………………………………7分
所以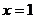 是
是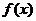 的唯一极小值点.极小值是
的唯一极小值点.极小值是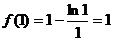 . ………………8分
. ………………8分
(3)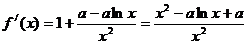 ,令
,令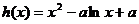
由题设,对任意 ,有
,有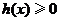 ,
,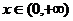 ,
,
又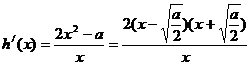 ……………………………………10分
……………………………………10分
当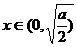 时,
时,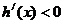 ,
,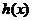 是减函数;当
是减函数;当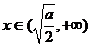 时,
时,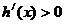 ,
,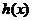 是增函数;所以当
是增函数;所以当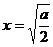 时,
时,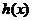 有极小值,也是最小值
有极小值,也是最小值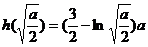 ,
,
………………………………………………12分
又由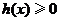 得
得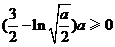 ,得
,得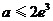 ,即
,即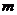 的最大值为
的最大值为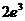 . ……14分
. ……14分
21.(本小题满分14分)
设函数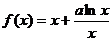 ,其中
,其中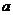 为常数.
为常数.
(1)证明:对任意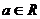 ,
,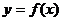 的图象恒过定点;
的图象恒过定点;
(2)当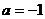 时,判断函数
时,判断函数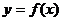 是否存在极值?若存在,求出极值;若不存在,说明理由;
是否存在极值?若存在,求出极值;若不存在,说明理由;
(3)若对任意 时,
时,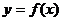 恒为定义域上的增函数,求
恒为定义域上的增函数,求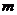 的最大值.
的最大值.
20.(本小题满分14分)
解:(1)由已知,圆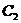 :
: 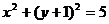 的圆
的圆
心为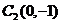 ,半径
,半径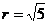 .……1分
.……1分
由题设圆心到直线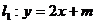 的距离
的距离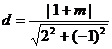 . ……………………3分
. ……………………3分
即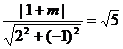 ,解得
,解得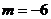 (
(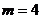 舍去). …………………………4分
舍去). …………………………4分
设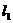 与抛物线的相切点为
与抛物线的相切点为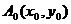 ,又
,又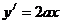 , ……………………………5分
, ……………………………5分
得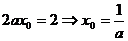 ,
,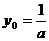 . ………………………………………………6分
. ………………………………………………6分
代入直线方程得: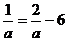 ,∴
,∴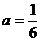
所以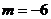 ,
,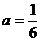 . ……………………………………………………………7分
. ……………………………………………………………7分
(2)由(1)知抛物线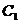 方程为
方程为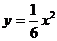 ,焦点
,焦点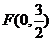 . ………………………8分
. ………………………8分
设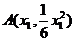 ,由(1)知以
,由(1)知以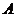 为切点的切线
为切点的切线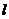 的方程为
的方程为
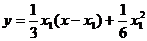 . …………………………………………………………10分
. …………………………………………………………10分
令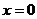 ,得切线
,得切线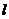 交
交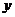 轴的
轴的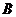 点坐标为
点坐标为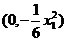 ……………………………11分
……………………………11分
所以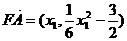 ,
,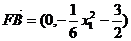 , ……………………………12分
, ……………………………12分
∴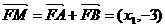 ……………………………………………………13分
……………………………………………………13分
因为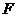 是定点,所以点
是定点,所以点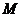 在定直线
在定直线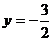 上. ………………………………14分
上. ………………………………14分
20.(本小题满分14分)
已知抛物线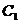 的方程为
的方程为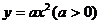 ,圆
,圆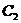 的方程为
的方程为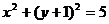 ,直线
,直线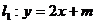 (
(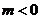 )是
)是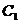 、
、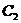 的公切线.
的公切线.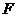 是
是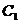 的焦点.
的焦点.
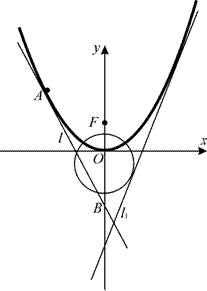 (1)求
(1)求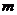 与
与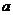 的值;
的值;
(2)设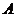 是
是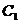 上的一动点,以
上的一动点,以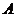 为切点的
为切点的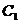 的切
的切
线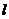 交
交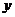 轴于点
轴于点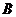 ,设
,设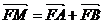 ,
,
证明:点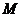 在一定直线上.
在一定直线上.
22.(本小题满分15分)
解:(I)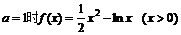
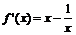 …………………………………………………………………………………3分
…………………………………………………………………………………3分
由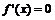 得
得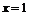
可得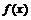 在(0,1)上单调递减,在(1,+∞)上单调递增……………………………5分
在(0,1)上单调递减,在(1,+∞)上单调递增……………………………5分
故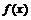 的最小值
的最小值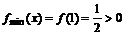 ,所以
,所以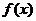 没有零点………………………………7分
没有零点………………………………7分
(II)方法一:
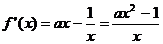 ………………………………………………………………9分
………………………………………………………………9分
(i)若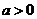 时,令
时,令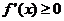 ,则
,则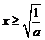 ,故
,故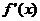 在
在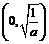 上单调递减,在
上单调递减,在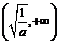 上单调递增,故
上单调递增,故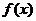 在
在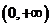 上的最小值为
上的最小值为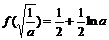 ,
,
要使解得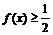 恒成立,只需
恒成立,只需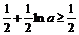 ,得
,得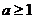 …………………………………12分
…………………………………12分
(ii)若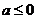 ,
,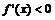 恒成立,
恒成立,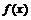 在
在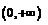 是单调递减,
是单调递减,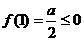 ,
,
故不可能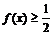 恒成立…………………………………………………………………….14分
恒成立…………………………………………………………………….14分
综上所述,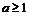 ……………………………………………………………………………….15分
……………………………………………………………………………….15分
方法二:由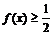 恒成立,得
恒成立,得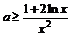 恒成立………………………………………….9分
恒成立………………………………………….9分
设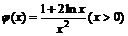 ,则
,则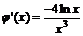 ……………………………………………….11分
……………………………………………….11分
由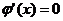 得
得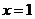 故
故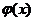 的最大值为
的最大值为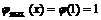 ………………………….13分
………………………….13分
要使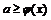 恒成立,只需
恒成立,只需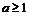 …………………………………………………………….15分
…………………………………………………………….15分
22.(本题满分15分)已知函数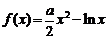 ,
,
(I) 若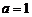 ,证明
,证明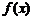 没有零点;
没有零点;
(II)若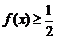 恒成立,求a的取值范围.
恒成立,求a的取值范围.
21.(本小题满分15分)
解:(I)由条件得抛物线方程为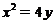 ……………………………………………………3分
……………………………………………………3分
∴把点A代入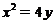 , 得
, 得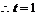 … ……………………………………6分
… ……………………………………6分
(II)设直线AP的斜率为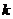 ,AQ的斜率为
,AQ的斜率为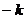 ,
,
则直线AP的方程为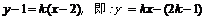
联立方程: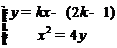
消去y,得: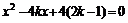 …………………………………………9分
…………………………………………9分
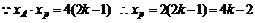
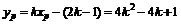
同理,得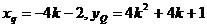 ………………………………………………12分
………………………………………………12分
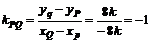 是一个与k无关的定值。………………………………………15分
是一个与k无关的定值。………………………………………15分
21.(本题满分15分)已知抛物线C的顶点在原点,焦点为F(0,1),且过点A(2,t),
(I)求t的值;
(II)若点P、Q是抛物线C上两动点,且直线AP与AQ的斜率互为相反数,试问直线PQ的斜率是否为定值,若是,求出这个值;若不是,请说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com