
题目列表(包括答案和解析)
5.A. [命题意图]本小题主要考查了考生对二项式定理的掌握情况,尤其是展开式的通项公式的灵活应用,以及能否区分展开式中项的系数与其二项式系数,同时也考查了考生的一些基本运算能力.
[解析]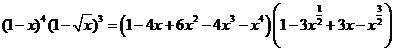
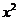 的系数是 -12+6=-6
的系数是 -12+6=-6
12、(2010全国卷1文数)(5)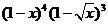 的展开式
的展开式 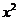 的系数是
的系数是
(A)-6 (B)-3 (C)0 (D)3
11、(2010福建文数)

9、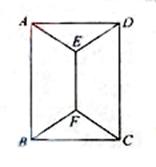 (2010天津理数)(10) 如图,用四种不同颜色给图中的A,B,C,D,E,F六个点涂色,要求每个点涂一种颜色,且图中每条线段的两个端点涂不同颜色,则不同的涂色方法用
(2010天津理数)(10) 如图,用四种不同颜色给图中的A,B,C,D,E,F六个点涂色,要求每个点涂一种颜色,且图中每条线段的两个端点涂不同颜色,则不同的涂色方法用
(A)288种 (B)264种 (C)240种 (D)168种
[答案]D
[解析]本题主要考查排列组合的基础知识与分类讨论思想,属于难题。
(1) B,D,E,F用四种颜色,则有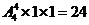 种涂色方法;
种涂色方法;
(2) B,D,E,F用三种颜色,则有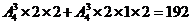 种涂色方法;
种涂色方法;
(3) B,D,E,F用两种颜色,则有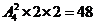 种涂色方法;
种涂色方法;
所以共有24+192+48=264种不同的涂色方法。
[温馨提示]近两年天津卷中的排列、组合问题均处理压轴题的位置,且均考查了分类讨论思想及排列、组合的基本方法,要加强分类讨论思想的训练。
8、(2010四川理数)(10)由1、2、3、4、5、6组成没有重复数字且1、3都不与5相邻的六位偶数的个数是
(A)72 (B)96 (C) 108 (D)144
解析:先选一个偶数字排个位,有3种选法
①若5在十位或十万位,则1、3有三个位置可排,3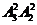 =24个
=24个
②若5排在百位、千位或万位,则1、3只有两个位置可排,共3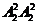 =12个
=12个
算上个位偶数字的排法,共计3(24+12)=108个
答案:C
7、(2010北京理数)(4)8名学生和2位第师站成一排合影,2位老师不相邻的排法种数为
(A)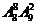 (B)
(B)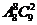 (C)
(C) 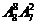 (D)
(D)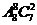
答案:A
6、(2010重庆理数)(9)某单位安排7位员工在10月1日至7日值班,每天1人,每人值班1天,若7位员工中的甲、乙排在相邻两天,丙不排在10月1日,丁不排在10月7日,则不同的安排方案共有
A. 504种 B. 960种 C. 1008种 D. 1108种
解析:分两类:甲乙排1、2号或6、7号 共有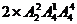 种方法
种方法
甲乙排中间,丙排7号或不排7号,共有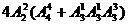 种方法
种方法
故共有1008种不同的排法
5、(2010重庆文数)(1)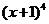 的展开式中
的展开式中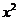 的系数为
的系数为
(A)4 (B)6
(C)10 (D)20
解析:由通项公式得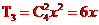
4、(2010重庆文数)(10)某单位拟安排6位员工在今年6月14日至16日(端午节假期)值班,每天安排2人,每人值班1天 . 若6位员工中的甲不值14日,乙不值16日,则不同的安排方法共有
(A)30种 (B)36种
(C)42种 (D)48种
解析:法一:所有排法减去甲值14日或乙值16日,再加上甲值14日且乙值16日的排法
即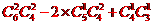 =42
=42
法二:分两类
甲、乙同组,则只能排在15日,有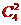 =6种排法
=6种排法
甲、乙不同组,有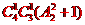 =36种排法,故共有42种方法
=36种排法,故共有42种方法
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com