
题目列表(包括答案和解析)
13.(2010湖南文数)图2中的三个直角三角形是一个体积为20cm2的几何体的三视图,则h= 4 cm
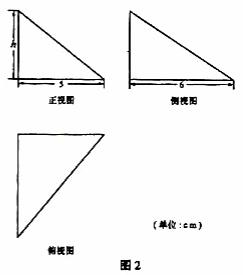
(2010浙江理数)(12)若某几何体的三视图(单位:cm)如图所示,则此几何体的体积是___________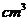 .
.
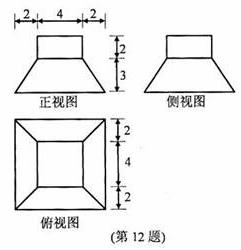 解析:图为一四棱台和长方体的组合体的三视图,由卷中所给公式计算得体积为144,本题主要考察了对三视图所表达示的空间几何体的识别以及几何体体积的计算,属容易题
解析:图为一四棱台和长方体的组合体的三视图,由卷中所给公式计算得体积为144,本题主要考察了对三视图所表达示的空间几何体的识别以及几何体体积的计算,属容易题
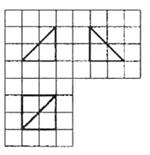 (2010辽宁文数)(16)如图,网格纸的小正方形的边长是1,在其上用粗线画
(2010辽宁文数)(16)如图,网格纸的小正方形的边长是1,在其上用粗线画
出了某多面体的三视图,则这个多面体最长的一条棱的
长为 .
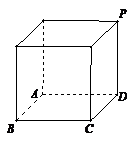 解析:填
解析:填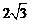 画出直观图:图中四棱锥
画出直观图:图中四棱锥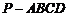 即是,
即是,
所以最长的一条棱的长为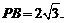
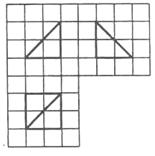 (2010辽宁理数)(15)如图,网格纸的小正方形的边长是1,在其上用粗线画出了某多面体的三视图,则这个多面体最长的一条棱的长为______.
(2010辽宁理数)(15)如图,网格纸的小正方形的边长是1,在其上用粗线画出了某多面体的三视图,则这个多面体最长的一条棱的长为______.
[答案]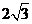
[命题立意]本题考查了三视图视角下多面体棱长的最值问题,考查了同学们的识图能力以及由三视图还原物体的能力。
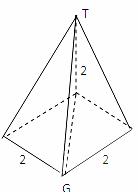
[解析]由三视图可知,此多面体是一个底面边长为2的正方形且有一条长为2的侧棱垂直于底面的四棱锥,所以最长棱长为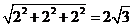
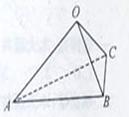 (2010江西理数)16.如图,在三棱锥
(2010江西理数)16.如图,在三棱锥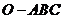 中,三条棱
中,三条棱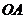 ,
,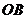 ,
,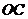 两两垂直,且
两两垂直,且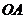 >
>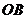 >
>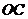 ,分别经过三条棱
,分别经过三条棱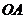 ,
,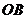 ,
,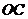 作一个截面平分三棱锥的体积,截面面积依次为
作一个截面平分三棱锥的体积,截面面积依次为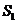 ,
,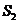 ,
,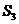 ,则
,则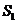 ,
,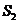 ,
, 的大小关系为
。
的大小关系为
。
[答案] 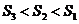
[解析]考查立体图形的空间感和数学知识的运用能力,通过补形,借助长方体验证结论,特殊化,令边长为1,2,3得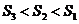 。
。
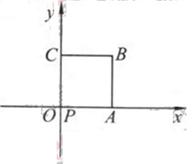 (2010北京文数)(14)如图放置的边长为1的正方形PABC沿x轴滚动。
(2010北京文数)(14)如图放置的边长为1的正方形PABC沿x轴滚动。
设顶点p(x,y)的纵坐标与横坐标的函数关系是
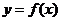 ,则
,则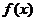 的最小正周期为
;
的最小正周期为
;
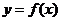 在其两个相邻零点间的图像与x轴
在其两个相邻零点间的图像与x轴
所围区域的面积为 。
说明:“正方形PABC沿x轴滚动”包含沿x轴正方向和沿x轴负方向滚动。沿x轴正方向滚动是指以顶点A为中心顺时针旋转,当顶点B落在x轴上时,再以顶点B为中心顺时针旋转,如此继续,类似地,正方形PABC可以沿着x轴负方向滚动。
答案:4 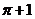
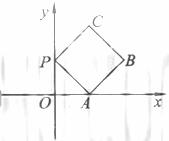 (2010北京理数)(14)如图放置的边长为1的正方形PABC沿x轴滚动。
(2010北京理数)(14)如图放置的边长为1的正方形PABC沿x轴滚动。
设顶点p(x,y)的轨迹方程是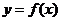 ,则
,则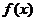 的最小正周期为
;
的最小正周期为
;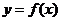 在其两个相邻零点间的图像与x轴所围区域的面积为
在其两个相邻零点间的图像与x轴所围区域的面积为
说明:“正方形PABC沿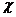 轴滚动”包括沿
轴滚动”包括沿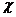 轴正方向和沿
轴正方向和沿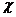 轴负方向滚动。沿
轴负方向滚动。沿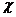 轴正方向滚动指的是先以顶点A为中心顺时针旋转,当顶点B落在
轴正方向滚动指的是先以顶点A为中心顺时针旋转,当顶点B落在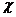 轴上时,再以顶点B为中心顺时针旋转,如此继续。类似地,正方形PABC可以沿
轴上时,再以顶点B为中心顺时针旋转,如此继续。类似地,正方形PABC可以沿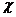 轴负方向滚动。
轴负方向滚动。
答案:4 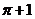
(2010四川理数)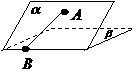 (15)如图,二面角
(15)如图,二面角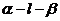 的大小是60°,线段
的大小是60°,线段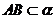 .
.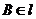 ,
,
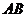 与
与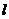 所成的角为30°.则
所成的角为30°.则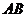 与平面
与平面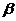 所成的角的正弦值是
.
所成的角的正弦值是
.
解析:过点A作平面β的垂线,垂足为C,在β内过C作l的垂线.垂足为D
连结AD,有三垂线定理可知AD⊥l,
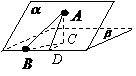 故∠ADC为二面角
故∠ADC为二面角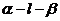 的平面角,为60°
的平面角,为60°
又由已知,∠ABD=30°
连结CB,则∠ABC为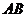 与平面
与平面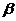 所成的角w_w_w.k*s 5*
所成的角w_w_w.k*s 5*
设AD=2,则AC=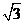 ,CD=1
,CD=1
AB=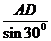 =4
=4
∴sin∠ABC=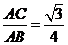
答案: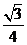
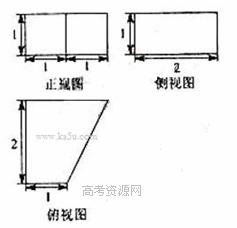 (2010天津文数)(12)一个几何体的三视图如图所示,则这个几何体的体积为
。
(2010天津文数)(12)一个几何体的三视图如图所示,则这个几何体的体积为
。
[答案]3
[解析]本题主要考查三视图的基础知识,和主题体积的计算,属于容易题。
由俯视图可知该几何体的底面为直角梯形,则正视图和俯视图可知该几何体的高为1,结合三个试图可知该几何体是底面为直角梯形的直四棱柱,所以该几何题的体积为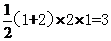
[温馨提示]正视图和侧视图的高是几何体的高,由俯视图可以确定几何体底面的形状,本题也可以将几何体看作是底面是长为3,宽为2,高为1的长方体的一半。
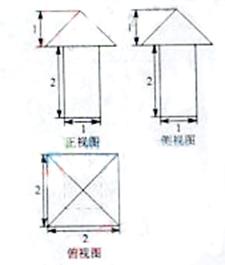 (2010天津理数)(12)一个几何体的三视图如图所示,则这个几何体的体积为
(2010天津理数)(12)一个几何体的三视图如图所示,则这个几何体的体积为
[答案]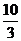
[解析]本题主要考查三视图的概念与柱体、椎体体积的计算,属于容易题。
由三视图可知,该几何体为一个底面边长为1,高为2的正四棱柱与一个底面边长为2,高为1的正四棱锥组成的组合体,因为正巳灵珠的体积为2,正四棱锥的体积为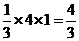 ,所以该几何体的体积V=2+
,所以该几何体的体积V=2+ 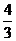 =
= 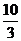
[温馨提示]利用俯视图可以看出几何体底面的形状,结合正视图与侧视图便可得到几何体的形状,求锥体体积时不要丢掉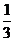 哦。
哦。
(2010四川文数)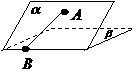 (15)如图,二面角
(15)如图,二面角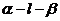 的大小是60°,线段
的大小是60°,线段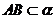 .
.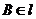 ,
,
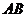 与
与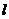 所成的角为30°.则
所成的角为30°.则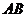 与平面
与平面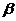 所成的角的正弦值是
.
所成的角的正弦值是
.
解析:过点A作平面β的垂线,垂足为C,在β内过C作l的垂线.垂足为D
连结AD,有三垂线定理可知AD⊥l,
故∠ADC为二面角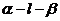 的平面角,为60°
的平面角,为60°
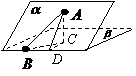 又由已知,∠ABD=30°
又由已知,∠ABD=30°
连结CB,则∠ABC为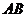 与平面
与平面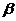 所成的角
所成的角
设AD=2,则AC=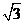 ,CD=1
,CD=1

 w_w w. k#s5_
w_w w. k#s5_
AB=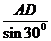 =4
=4
∴sin∠ABC=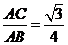
答案: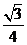


 w_w w. k#s5_
w_w w. k#s5_

6.(2010上海文数)已知四棱椎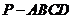 的底面是边长为6 的正方形,侧棱
的底面是边长为6 的正方形,侧棱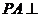 底面
底面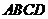 ,且
,且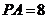 ,则该四棱椎的体积是 96 。
,则该四棱椎的体积是 96 。
解析:考查棱锥体积公式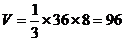
11.[答案]6
[解析]二项式展开式的通项公式为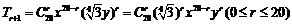 要使系数为有理数,则r必为4的倍数,所以r可为0.、4、8、12、16、20共6种,故系数为有理数的项共有6项.
要使系数为有理数,则r必为4的倍数,所以r可为0.、4、8、12、16、20共6种,故系数为有理数的项共有6项.
(2010安徽卷理)

11、(2010湖北理数)在(x+ 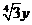 )
)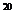 的展开式中,系数为有理数的项共有_______项。
的展开式中,系数为有理数的项共有_______项。
11.(2010湖北文数)在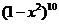 的展开中,
的展开中, 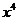 的系数为______。
的系数为______。
[答案]45
[解析]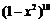 展开式即是10个(1-x2)相乘,要得到x4,则取2个1-x2中的(-x2)相乘,其余选1,则系数为
展开式即是10个(1-x2)相乘,要得到x4,则取2个1-x2中的(-x2)相乘,其余选1,则系数为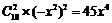 ,故系数为45.
,故系数为45.
15. A[命题意图]本小题主要考查分类计数原理、组合知识,以及分类讨论的数学思想.
[解析1]:可分以下2种情况:(1)A类选修课选1门,B类选修课选2门,有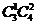 种不同的选法;(2)A类选修课选2门,B类选修课选1门,有
种不同的选法;(2)A类选修课选2门,B类选修课选1门,有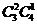 种不同的选法.所以不同的选法共有
种不同的选法.所以不同的选法共有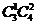 +
+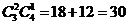 种.
种.
[解析2]: 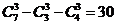
(2010四川文数)(13)(x-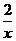 )4的展开式中的常数项为______________(用数字作答)
)4的展开式中的常数项为______________(用数字作答)
解析:展开式的通项公式为Tr+1=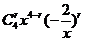
取r=2得常数项为C42(-2)2=24

 w_w w. k#s5_
w_w w. k#s5_
答案:24
14.(2010江西理数)将6位志愿者分成4组,其中两个各2人,另两个组各1人,分赴世博会的四个不同场馆服务,不同的分配方案有 种(用数字作答)。
[答案] 1080
[解析]考查概率、平均分组分配问题等知识,重点考查化归转化和应用知识的意识。先分组,考虑到有2个是平均分组,得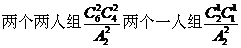 ,再全排列得:
,再全排列得:
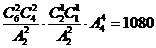
(2010四川理数)(13)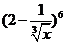 的展开式中的第四项是
. w_w_w.k*s 5*
的展开式中的第四项是
. w_w_w.k*s 5*
解析:T4=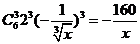 w_w_w.k*s 5*
w_w_w.k*s 5*
答案:-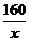
(2010天津理数)(11)甲、乙两人在10天中每天加工零件的个数用茎叶图表示如下图,中间一列的数字表示零件个数的十位数,两边的数字表示零件个数的个位数,则这10天甲、乙两人日加工零件的平均数分别为 和 。
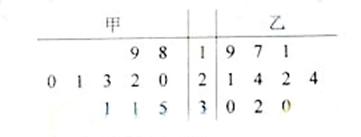
[答案]24,23
[解析]本题主要考查茎叶图的应用,属于容易题。
甲加工零件个数的平均数为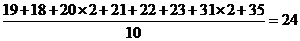
乙加工零件个数的平均数为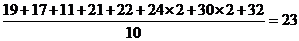
[温馨提示]茎叶图中共同的数字是数字的十位,这事解决本题的突破口。
(2010全国卷1文数)(15)某学校开设A类选修课3门,B类选修课4门,一位同学从中共选3门,若要求两类课程中各至少选一门,则不同的选法共有 种.(用数字作答)
5.(2010上海文数)将一个总数为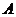 、
、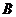 、
、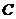 三层,其个体数之比为5:3:2。若用分层抽样方法抽取容量为100的样本,则应从
三层,其个体数之比为5:3:2。若用分层抽样方法抽取容量为100的样本,则应从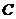 中抽取 20 个个体。
中抽取 20 个个体。
解析:考查分层抽样应从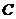 中抽取
中抽取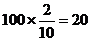
(2010浙江理数)(17)有4位同学在同一天的上、下午参加“身高与体重”、“立定跳远”、“肺活量”、“握力”、“台阶”五个项目的测试,每位同学上、下午各测试一个项目,且不重复. 若上午不测“握力”项目,下午不测“台阶”项目,其余项目上、下午都各测试一人. 则不同的安排方式共有______________种(用数字作答).
解析:本题主要考察了排列与组合的相关知识点,突出对分类讨论思想和数学思维能力的考察,属较难题
(2010全国卷2理数)(14)若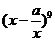 的展开式中
的展开式中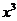 的系数是
的系数是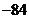 ,则
,则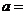 .
.
[答案]1
[命题意图]本试题主要考查二项展开式的通项公式和求指定项系数的方法.
[解析]展开式中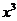 的系数是
的系数是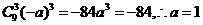 .
.
(2010辽宁理数)(13)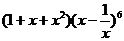 的展开式中的常数项为_________.
的展开式中的常数项为_________.
[答案]-5
[命题立意]本题考查了二项展开式的通项,考查了二项式常数项的求解方法
[解析]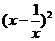 的展开式的通项为
的展开式的通项为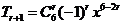 ,当r=3时,
,当r=3时,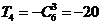 ,当r=4时,
,当r=4时,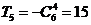 ,因此常数项为-20+15=-5
,因此常数项为-20+15=-5
(2010全国卷2文数)(14)(x+1/x)9的展开式中,x3的系数是_________
[解析]84:本题考查了二项展开式定理的基础知识
∵ 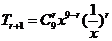 ,∴
,∴ 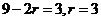 ,∴
,∴ 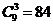
12.(2010上海文数)在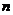 行
行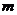 列矩阵
列矩阵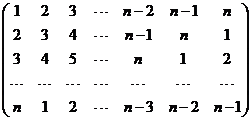 中,
中,
记位于第 行第
行第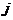 列的数为
列的数为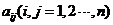 。当
。当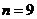 时,
时,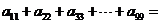 45 。
45 。
解析: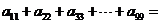 1+3+5+7+9+2+4+6+8=45
1+3+5+7+9+2+4+6+8=45
11.(2010上海文数) 2010年上海世博会园区每天9:00开园,20:00停止入园。在右边的框图中,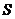 表示上海世博会官方网站在每个整点报道的入园总人数,
表示上海世博会官方网站在每个整点报道的入园总人数,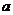 表示整点报道前1个小时内入园人数,则空白的执行框内应填入 S←S+a 。
表示整点报道前1个小时内入园人数,则空白的执行框内应填入 S←S+a 。
解析:考查算法
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com