
题目列表(包括答案和解析)
3.已知函数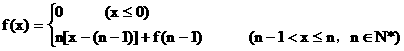 ,数列
,数列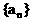 满足
满足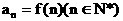
(I)求数列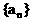 的通项公式;(II)设x轴、直线
的通项公式;(II)设x轴、直线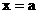 与函数
与函数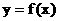 的图象所围成的封闭图形的面积为
的图象所围成的封闭图形的面积为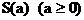 ,求
,求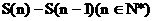 ;(III)在集合
;(III)在集合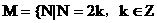 ,且
,且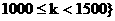 中,是否存在正整数N,使得不等式
中,是否存在正整数N,使得不等式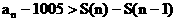 对一切
对一切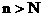 恒成立?若存在,则这样的正整数N共有多少个?并求出满足条件的最小的正整数N;若不存在,请说明理由.(IV)请构造一个与
恒成立?若存在,则这样的正整数N共有多少个?并求出满足条件的最小的正整数N;若不存在,请说明理由.(IV)请构造一个与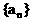 有关的数列
有关的数列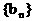 ,使得
,使得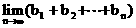 存在,并求出这个极限值
存在,并求出这个极限值 *5U.C#O%
*5U.C#O%
解:(I)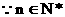
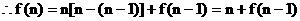
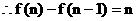 ……1分
……1分
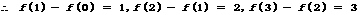 ……
…… 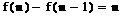 ,将这n个式子相加,得
,将这n个式子相加,得
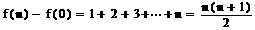
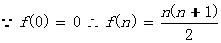
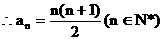 …3分
…3分
(II)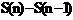 为一直角梯形(
为一直角梯形(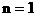 时为直角三角形)的面积,该梯形的两底边的长分别为
时为直角三角形)的面积,该梯形的两底边的长分别为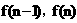 ,高为1
,高为1
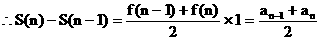
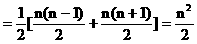
(III)设满足条件的正整数N存在,则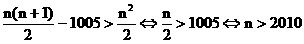
又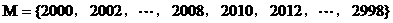 K^S*5U.C#O%
K^S*5U.C#O%
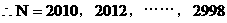 均满足条件,它们构成首项为2010,公差为2的等差数列.
均满足条件,它们构成首项为2010,公差为2的等差数列.
设共有m个满足条件的正整数N,则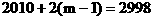 ,解得
,解得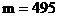
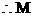 中满足条件的正整数N存在,共有495个,
中满足条件的正整数N存在,共有495个,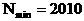 ……9分
……9分
(IV)设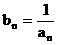 ,即
,即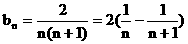 K^S*5U.C#O%
K^S*5U.C#O%
则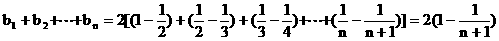
显然,其极限存在,并且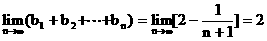 ……10分
……10分
注: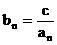 (c为非零常数),
(c为非零常数),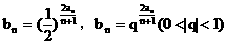 等都能使
等都能使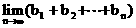 存在.
存在.
2.设M是椭圆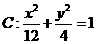 上的一点,P、Q、T分别为M关于y轴、原点、x轴的对称点,N为椭圆C上异于的另一点,且MN⊥MQ,QN与PT的交点为E,当M沿椭圆C运动时,求动点E的轨迹方程
上的一点,P、Q、T分别为M关于y轴、原点、x轴的对称点,N为椭圆C上异于的另一点,且MN⊥MQ,QN与PT的交点为E,当M沿椭圆C运动时,求动点E的轨迹方程
解:设点的坐标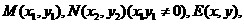 则
则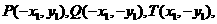 ……1分
……1分
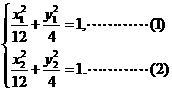 ………3分由(1)-(2)可得
………3分由(1)-(2)可得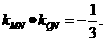 …………6分
…………6分
又MN⊥MQ,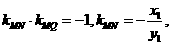 所以
所以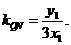
直线QN的方程为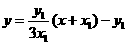 ,又直线PT的方程为
,又直线PT的方程为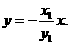 ……10分
……10分
从而得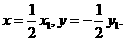 所以
所以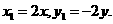
代入(1)可得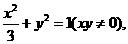 此即为所求的轨迹方程.………………13分
此即为所求的轨迹方程.………………13分
1.已知点P ( t , y )在函数f ( x ) = 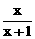 (x
¹ –1)的图象上,且有t2 – c2at
+ 4c2 = 0 ( c ¹
0 ).
(x
¹ –1)的图象上,且有t2 – c2at
+ 4c2 = 0 ( c ¹
0 ).
(1) 求证:| ac | ³ 4;(2) 求证:在(–1,+∞)上f ( x )单调递增.(3)求证:f ( | a | ) + f ( | c | ) > 1.
证:(1) ∵ tÎR, t ¹ –1, ∴ ⊿ = (–c2a)2 – 16c2 = c4a2 – 16c2 ³ 0 ,
∵ c ¹ 0, ∴c2a2 ³ 16 , ∴| ac | ³ 4.
(2) 由 f ( x )
= 1 – 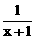 ,
,
法1. 设–1 < x1 < x2, 则f
(x2) – f ( x1) = 1– 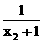 –1
+
–1
+ 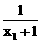 =
=
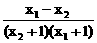 .
.
∵ –1 < x1 < x2, ∴ x1 – x2 < 0, x1 + 1 > 0, x2 + 1 > 0 ,
∴f (x2) – f ( x1) < 0 , 即f (x2) < f ( x1) , ∴x ³ 0时,f ( x )单调递增.
法2. 由f ` ( x ) = 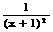 > 0 得x ¹
–1, ∴x > –1时,f ( x )单调递增.
> 0 得x ¹
–1, ∴x > –1时,f ( x )单调递增.
(3)∵f ( x )在x > –1时单调递增,| c | ³ 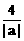 > 0 , ∴f (| c |
) ³ f (
> 0 , ∴f (| c |
) ³ f (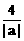 ) =
) = 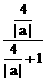 =
= 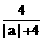
f ( | a | ) + f ( | c | ) =
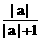 +
+ 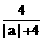 >
> 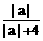 +
+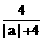 =1.即f ( | a | ) + f ( | c | )
> 1.
=1.即f ( | a | ) + f ( | c | )
> 1.
例3、求直线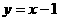 被抛物线
被抛物线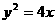 截得线段的中点坐标。
截得线段的中点坐标。
解:解法一:设直线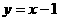 与抛物线
与抛物线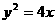 交于
交于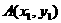 ,
, 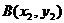 ,其中点
,其中点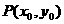 ,由题意得
,由题意得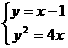 ,
,
消去y得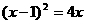 ,即
,即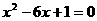 ,
,
所以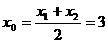 ,
,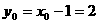 ,即中点坐标为
,即中点坐标为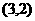 。
。
解法二:设直线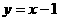 与抛物线
与抛物线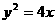 交于
交于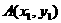 ,
, 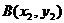 ,其中点
,其中点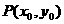 ,由题意得
,由题意得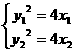 ,两式相减得
,两式相减得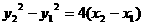 ,
,
所以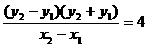 ,
,
所以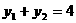 ,即
,即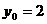 ,
, ,即中点坐标为
,即中点坐标为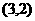 。
。
上面我们给出了解决直线与圆锥曲线相交所得弦中点问题的一些基本解法。下面我们看一个结论
引理 设A、B是二次曲线C: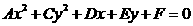 上的两点,P
上的两点,P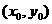 为弦AB的中点,则
为弦AB的中点,则
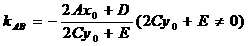 。
。
设A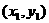 、B
、B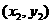 则
则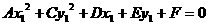 ……(1)
……(1)
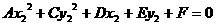 ……(2)
……(2)
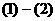 得
得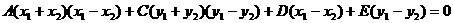
∴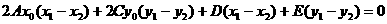
∴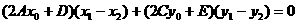
∵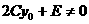 ∴
∴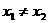 ∴
∴
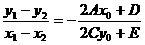 即
即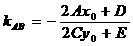 。(说明:当
。(说明:当 时,上面的结论就是过二次曲线C上的点P
时,上面的结论就是过二次曲线C上的点P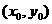 的切线斜率公式,即
的切线斜率公式,即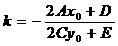 )
)
推论1 设圆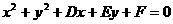 的弦AB的中点为P
的弦AB的中点为P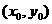 (
(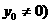 ,则
,则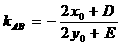 。(假设点P在圆上时,则过点P的切线斜率为
。(假设点P在圆上时,则过点P的切线斜率为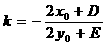 )
)
推论2 设椭圆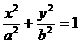 的弦AB的中点为P
的弦AB的中点为P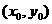 (
(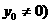 ,则
,则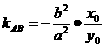 。(注:对a≤b也成立。假设点P在椭圆上,则过点P的切线斜率为
。(注:对a≤b也成立。假设点P在椭圆上,则过点P的切线斜率为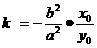 )
)
推论3 设双曲线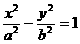 的弦AB的中点为P
的弦AB的中点为P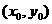 (
(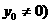 则
则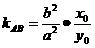 。(假设点P在双曲线上,则过P点的切线斜率为
。(假设点P在双曲线上,则过P点的切线斜率为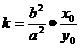 )
)
推论4 设抛物线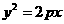 的弦AB的中点为P
的弦AB的中点为P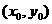 (
(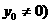 则
则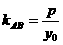 。(假设点P在抛物线上,则过点P的切线斜率为
。(假设点P在抛物线上,则过点P的切线斜率为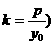
我们可以直接应用上面这些结论解决有关问题,下面举例说明。
例1、求椭圆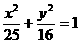 斜率为3的弦的中点轨迹方程。
斜率为3的弦的中点轨迹方程。
解:设P(x,y)是所求轨迹上的任一点,则有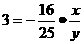 ,故所示的轨迹方程为16x+75y=0
,故所示的轨迹方程为16x+75y=0 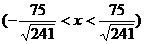
例2、已知椭圆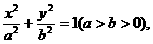 A、B是椭圆上两点,线段AB的垂直平分线l与x轴相交于P
A、B是椭圆上两点,线段AB的垂直平分线l与x轴相交于P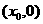 ,求证:
,求证: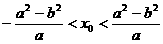 。
。
证明:设AB的中点为T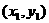 ,由题设可知AB与x轴不垂直,∴
,由题设可知AB与x轴不垂直,∴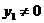 ,
,
∴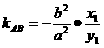 ∵l⊥AB ∴
∵l⊥AB ∴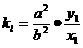
∴l的方程为: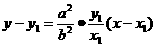 令y=0 得
令y=0 得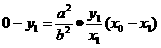
∴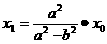 ∵
∵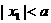 ∴
∴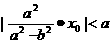
∴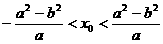
例3、已知抛物线C: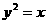 ,直线
,直线
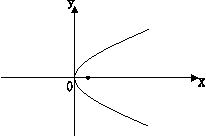
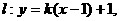 要使抛物线C上存
要使抛物线C上存
在关于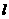 对称的两点,
对称的两点,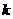 的取值范围是什么?
的取值范围是什么?
解:设C上两点A、B两点关于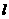 对称,AB的
对称,AB的
中点为P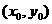 (
(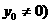
∴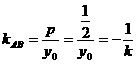 ∴
∴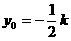 ∵P∈
∵P∈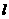 ∴
∴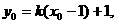
∴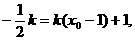 ∴
∴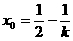 ∴
∴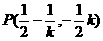
∵P在抛物线内 ,∴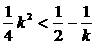 ∴
∴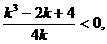
∴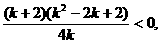 ∴
∴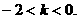
例2、过椭圆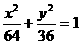 上一点P(-8,0)作直线交椭圆于Q点,求PQ中点的轨迹方程。
上一点P(-8,0)作直线交椭圆于Q点,求PQ中点的轨迹方程。
解法一:设弦PQ中点M(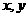 ),弦端点P(
),弦端点P(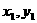 ),Q(
),Q(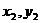 ),
),
则有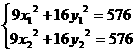 ,
,
两式相减得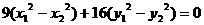 ,
,
又因为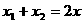 ,
,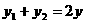 ,所以
,所以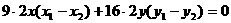 ,
,
所以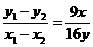 ,
,
而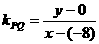 ,故
,故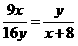 。
。
化简可得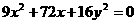 (
(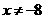 )。
)。
解法二:设弦中点M(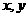 ),Q(
),Q(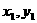 ),
),
由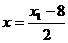 ,
,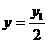 可得
可得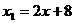 ,
,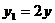 ,
,
又因为Q在椭圆上,所以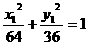 ,
,
即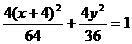 ,
,
所以PQ中点M的轨迹方程为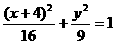 (
(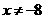 )。
)。
例1、过椭圆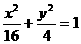 内一点M(2,1)引一条弦,使弦被点M平分,求这条弦所在的直线方程。
内一点M(2,1)引一条弦,使弦被点M平分,求这条弦所在的直线方程。
解法一:设所求直线方程为y-1=k(x-2),代入椭圆方程并整理得:
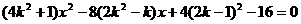
又设直线与椭圆的交点为A(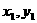 ),B(
),B(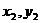 ),则
),则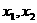 是方程的两个根,于是
是方程的两个根,于是
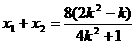 ,
,
又M为AB的中点,所以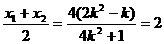 ,
,
解得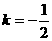 ,
,
故所求直线方程为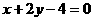 。
。
解法二:设直线与椭圆的交点为A(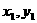 ),B(
),B(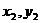 ),M(2,1)为AB的中点,
),M(2,1)为AB的中点,
所以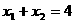 ,
,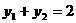 ,
,
又A、B两点在椭圆上,则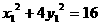 ,
,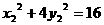 ,
,
两式相减得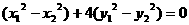 ,
,
所以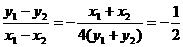 ,即
,即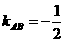 ,
,
故所求直线方程为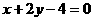 。
。
解法三:设所求直线与椭圆的一个交点为A(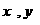 ),由于中点为M(2,1),
),由于中点为M(2,1),
则另一个交点为B(4-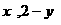 ),
),
因为A、B两点在椭圆上,所以有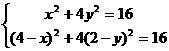 ,
,
两式相减得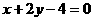 ,
,
由于过A、B的直线只有一条,
故所求直线方程为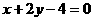 。
。
24、若直线l: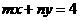 与圆
与圆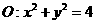 没有公共点,则过点
没有公共点,则过点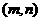 的直线与椭圆
的直线与椭圆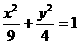 的公共点个数为 .
的公共点个数为 .
23、已知实数x,y满足条件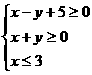 ,
,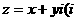 为虚数单位),则
为虚数单位),则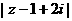 的最大值和最小值分别是 。
的最大值和最小值分别是 。
22、一个总体共有100个个体,随机编号0,1,2,…,99,按从小到大的编号顺序平均分成10个小组,组号依次为1,2,3,…,10,现用系统抽样方法抽取一个容量为10的样本,规定如果在第1组随机抽取的号码为m,那么在第k组中抽取的号码个位数字与m+k的个位数字相同,若m=4,则在第6组中抽取的号码是
21、一几何体的三视图如下,它的体积为 。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com