5.(浙江卷理17)有4位同学在同一天的上、下午参加“身高与体重”、“立定跳远”、“肺活量”、“握力”、“台阶”五个项目的测试，每位同学上、下午各测试一个项目，且不重复. 若上午不测“握力”项目，下午不测“台阶”项目，其余项目上、下午都各测试一人. 则不同的安排方式共有______________种(用数字作答).

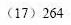
解析：本题主要考察了排列与组合的相关知识点，突出对分类讨论思想和数学思维能力的考察，属较难题

4.(上海卷理14)以集合U=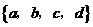的子集中选出4个不同的子集，需同时满足以下两个条件：(1)a、b都要选出；(2)对选出的任意两个子集A和B，必有，那么共有　　　　　　 种不同的选法。　

3.(全国Ⅰ卷文15)某学校开设A类选修课3门，B类选修课4门，一位同学从中共选3门，若要求两类课程中各至少选一门，则不同的选法共有　　　　　 种.(用数字作答)

[命题意图]本小题主要考查分类计数原理、组合知识,以及分类讨论的数学思想.

[解析1]:可分以下2种情况:(1)A类选修课选1门,B类选修课选2门,有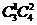种不同的选法;(2)A类选修课选2门,B类选修课选1门,有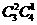种不同的选法.所以不同的选法共有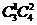+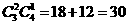种.

[解析2]: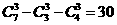

2. (江西卷文14)将5位志愿者分成3组，其中两组各2人，另一组1人，分赴世博会的三个不同场馆服务，不同的分配方案有　　　　　 种(用数字作答)；

[答案]90

[解析]考查排列组合里分组分配问题，

1.(江西卷理14)将6位志愿者分成4组，其中两个组各2人，另两个组各1人，分赴世博会的四个不同场馆服务，不同的分配方案有　　　 　　　种(用数字作答).

[答案] 1080

[解析]考查概率、平均分组分配问题等知识，重点考查化归转化和应用知识的意识。先分组，考虑到有2个是平均分组，得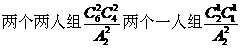，再全排列得：

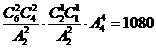
13.(重庆卷文10)某单位拟安排6位员工在今年6月14日至16日(端午节假期)值班，每天安排2人，每人值班1天。若6位员工中的甲不值14日，乙不值16日，则不同的安排方法共有

(A)30种　 　　　　(B)36种　 　　　　(C)42种　　 　　(D)48种

[答案]C

[解析]法一：所有排法减去甲值14日或乙值16日，再加上甲值14日且乙值16日的排法

　　　　　　 即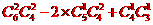=42

　　　 法二：分两类: 甲、乙同组，则只能排在15日，有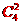=6种排法

　　　　　 甲、乙不同组，有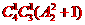=36种排法，故共有42种方法.

12.(重庆卷理9)某单位安排7位员工在10月1日至7日值班，每天1人，每人值班1天，若7位员工中的甲、乙排在相邻两天，丙部排在10月1日，也不排在10月7日，则不同的安排方案共有

A. 504种　　 　　　B. 960种　 　　　C. 1008种　　 　　D. 1108种　　　

[答案]C

解析：分两类：甲乙排1、2号或6、7号 共有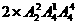种方法

甲乙排中间,丙排7号或不排7号，共有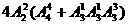种方法

故共有1008种不同的排法

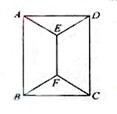
11.(天津卷理10)如图，用四种不同颜色给图中的A,B,C,D,E,F六个点涂色，要求每个点涂一种颜色，且图中每条线段的两个端点涂不同颜色，则不同的涂色方法用

(A)288种　　　 (B)264种　　　 (C)240种　　　 (D)168种

[答案]B

[解析]分三类：(1)B、D、E、F用四种颜色，则有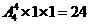种方法；

(2)B、D、E、F用三种颜色，则有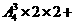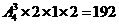种方法；

(3)B、D、E、F用二种颜色，则有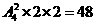，所以共有不同的涂色方法

24+192+48=264种。

[命题意图]本小题考查排列组合的基础知识，考查分类讨论的数学思想，有点难度。

10.(四川卷文9)由1、2、3、4、5组成没有重复数字且1、2都不与5相邻的五位数的个数是

(A)36　 　　　　　(B)32　 　　　　(C)28　 　　　　　(D)24

解析：如果5在两端，则1、2有三个位置可选，排法为2×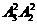＝24种,　 如果5不在两端，则1、2只有两个位置可选，3×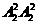＝12种

　　 共计12+24＝36种

答案：A

9.(四川卷理10)由1、2、3、4、5、6组成没有重复数字且1、3都不与5相邻的六位偶数的个数是

(A)72　　 　　　　(B)96　　　　 　　　(C) 108　　 　　　　(D)144

解析：先选一个偶数字排个位，有3种选法

①若5在十位或十万位，则1、3有三个位置可排，3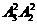＝24个

②若5排在百位、千位或万位，则1、3只有两个位置可排，共3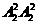＝12个

算上个位偶数字的排法，共计3(24+12)＝108个

答案：C