
题目列表(包括答案和解析)
25.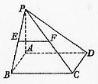 (陕西卷文18)如图,在四棱锥P-ABCD中,底面ABCD是矩形PA⊥平面ABCD,AP=AB,BP=BC=2,E,F分别是PB,PC的中点.
(陕西卷文18)如图,在四棱锥P-ABCD中,底面ABCD是矩形PA⊥平面ABCD,AP=AB,BP=BC=2,E,F分别是PB,PC的中点.
(Ⅰ)证明:EF∥平面PAD;
(Ⅱ)求三棱锥E-ABC的体积V.
解 (Ⅰ)在△PBC中,E,F分别是PB,PC的中点,∴EF∥BC.
又BC∥AD,∴EF∥AD,
又∵AD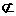 平面PAD,EF
平面PAD,EF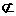 平面PAD,
平面PAD,
∴EF∥平面PAD.
(Ⅱ)连接AE,AC,EC,过E作EG∥PA交AB于点G,
则BG⊥平面ABCD,且EG=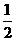 PA.
PA.
在△PAB中,AD=AB,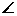 PAB°,BP=2,∴AP=AB=
PAB°,BP=2,∴AP=AB= ,EG=
,EG=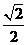 .
.
∴S△ABC=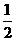 AB·BC=
AB·BC=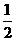 ×
× ×2=
×2= ,
,
∴VE-ABC=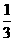 S△ABC·EG=
S△ABC·EG=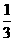 ×
× ×
×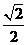 =
=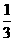 .
.
24.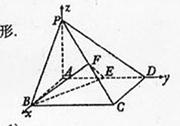 (陕西卷理18)如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA ⊥平面ABCD,AP=AB=2,BC=2 √ 2,E,F分别是AD,PC的重点
(陕西卷理18)如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA ⊥平面ABCD,AP=AB=2,BC=2 √ 2,E,F分别是AD,PC的重点
(Ⅰ)证明:PC ⊥平面BEF;
(Ⅱ)求平面BEF与平面BAP夹角的大小。
解法一
(Ⅰ)如图,以A为坐标原点,AB,AD,AP算在直线分别为x,y,z轴建立空间直角坐标系。
∵AP=AB=2,BC=AD=2√ 2,四边形ABCD是矩形。
∴A,B,C,D的坐标为A(0,0,0),B(2,0,0),C(2, 2 √ 2,0),D(0,2 √ 2,0),P(0,0,2)
又E,F分别是AD,PC的中点,
∴E(0,√ 2,0),F(1,√ 2,1)。
∴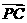 =(2,2 √ 2,-2)
=(2,2 √ 2,-2)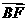 =(-1,√ 2,1)
=(-1,√ 2,1)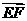 =(1,0, 1),
=(1,0, 1),
∴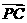 ·
·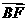 =-2+4-2=0,
=-2+4-2=0,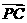 ·
·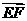 =2+0-2=0,
=2+0-2=0,
∴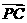 ⊥
⊥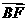 ,
,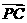 ⊥
⊥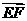 ,
,
∴PC⊥BF,PC⊥EF,BF ∩ EF=F,
∴PC⊥平面BEF


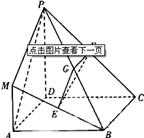
23.(山东卷文20)在如图所示的几何体中,四边形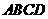 是正方形,
是正方形,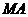
 平面
平面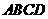 ,
,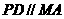 ,
,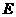 、
、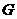 、
、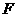 分别为
分别为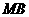 、
、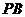 、
、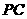 的中点,且
的中点,且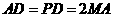 .
.
(I)求证:平面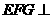 平面
平面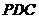 ;
;
(II)求三棱锥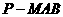 与四棱锥
与四棱锥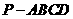 的体积之比.
的体积之比.
[命题意图]本小题主要考查空间中的线面关系,考查线面垂直、面面垂直的判定及几何体体积的计算,考查试图能力和逻辑思维能力。
[解析](I)证明:由已知MA 平面ABCD,PD ∥MA,
所以 PD∈平面ABCD
又 BC ∈ 平面ABCD,
因为 四边形ABCD为正方形,
所以 PD⊥ BC
又 PD∩DC=D,
因此 BC⊥平面PDC
在△PBC中,因为G平分为PC的中点,
所以 GF∥BC
因此 GF⊥平面PDC
又 GF ∈平面EFG,
所以 平面EFG⊥平面PDC.
(Ⅱ )解:因为PD⊥平面ABCD,四边形ABCD为正方形,不妨设MA=1,
则 PD=AD=2,ABCD
所以 Vp-ABCD=1/3S正方形ABCD,PD=8/3
由于 DA⊥面MAB的距离
所以 DA即为点P到平面MAB的距离,
三棱锥 Vp-MAB=1/3×1/2×1×2×2=2/3,所以 Vp-MAB:Vp-ABCD=1:4。
22.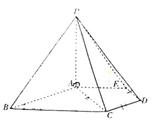 (山东卷理19)如图,在五棱锥P-ABCDE中,PA⊥平面ABCDE,AB∥CD,AC∥ED,AE∥BC,∠ABC=45。。AB=2
(山东卷理19)如图,在五棱锥P-ABCDE中,PA⊥平面ABCDE,AB∥CD,AC∥ED,AE∥BC,∠ABC=45。。AB=2 ,BC=2AE=4,三角形PAB是等腰三角形。
,BC=2AE=4,三角形PAB是等腰三角形。
(Ⅰ)求证:平面PCD⊥平面PAC;
(Ⅱ)求直线PB与平面PCD所成角的大小;
(Ⅲ)求四棱锥P-ACDE的体积。
[解析](Ⅰ)证明:因为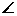 ABC=45°,AB=2
ABC=45°,AB=2 ,BC=4,所以在
,BC=4,所以在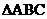 中,由余弦定理得:
中,由余弦定理得: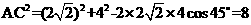 ,解得
,解得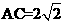 ,
,
所以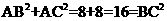 ,即
,即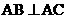 ,又PA⊥平面ABCDE,所以PA⊥
,又PA⊥平面ABCDE,所以PA⊥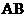 ,
,
又PA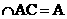 ,所以
,所以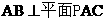 ,又AB∥CD,所以
,又AB∥CD,所以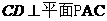 ,又因为
,又因为
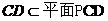 ,所以平面PCD⊥平面PAC;
,所以平面PCD⊥平面PAC;
(Ⅱ)由(Ⅰ)知平面PCD⊥平面PAC,所以在平面PAC内,过点A作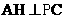 于H,则
于H,则
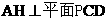 ,又AB∥CD,AB
,又AB∥CD,AB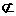 平面
平面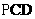 内,所以AB平行于平面
内,所以AB平行于平面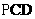 ,所以点A到平面
,所以点A到平面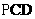 的距离等于点B到平面
的距离等于点B到平面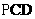 的距离,过点B作BO⊥平面
的距离,过点B作BO⊥平面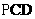 于点O,则
于点O,则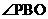 为所求角,且
为所求角,且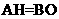 ,又容易求得
,又容易求得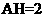 ,所以
,所以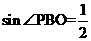 ,即
,即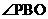 =
= ,所以直线PB与平面PCD所成角的大小为
,所以直线PB与平面PCD所成角的大小为 ;
;
(Ⅲ)由(Ⅰ)知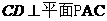 ,所以
,所以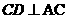 ,又AC∥ED,所以四边形ACDE是直角梯形,又容易求得
,又AC∥ED,所以四边形ACDE是直角梯形,又容易求得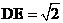 ,AC=
,AC=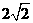 ,所以四边形ACDE的面积为
,所以四边形ACDE的面积为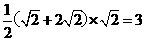 ,所以
,所以
四棱锥P-ACDE的体积为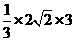 =
=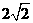 。
。
[命题意图]本题考查了空间几何体的的线面与面面垂直、线面角的求解以及几何体的体积计算问题,考查了同学们的空间想象能力以及空间思维能力。
(标准答案) 本小题主要考察空间中的基本关系,考察线面垂直、面面垂直的判定以及线面角和集合体体积的计算,考查识图能力、空间想象力和逻辑推理能力,满分12分
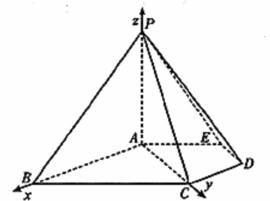
(|)证明:在△ABC中,因为∠ABC=45°,BC=4,AB=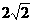 ,
,
所以AC2=AB+BC2-2AB·BC·cos45°=8
 因此 AC=
因此 AC=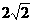 ,故BC2=AC2+AB2,所以∠BAC=90°
,故BC2=AC2+AB2,所以∠BAC=90°
所以CD⊥PA,CD⊥AC,
又 PA,AC  平面PAC,且PA
平面PAC,且PA AC=A,
AC=A,
所以 CD⊥PAC,又 CD 平面PCD,
平面PCD,
所以 平面PCD⊥平面PAC--------------------------------------------

则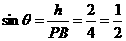 ,又
,又
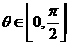 ,所以
,所以
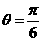
解法二:由(|)知AB,AC,AP两两相互垂直,分别以AB、AC、AP为x轴、y轴、z轴建立如图所示的空间直角坐标系,由于△PAB是等腰三角形,
所以 PA=AB=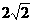 ,又AC=
,又AC=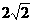 ,
,


因此直线PB与平面PCD所成的角为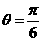
(Ⅲ)因为AC∥ED,CD⊥AC,所以 四边形ACDE是直角梯形,
因为 AE=2,∠ABC=45°,AE∥BC,
所以 ∠BAE=135°,因此 ∠CAE=45°,
故 CD=AE·sin45°==2×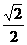 =
=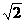 ,
,
所以 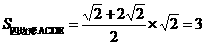
又 PA⊥平面ABCDE,
 所以
所以 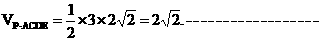
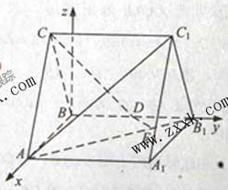
21.(全国Ⅱ卷理19文19)如图,直三棱柱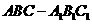 中,
中,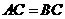 ,
,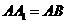 ,
,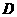 为
为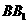 的中点,
的中点,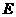 为
为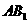 上的一点,
上的一点,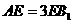 .
.
(Ⅰ)证明: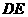 为异面直线
为异面直线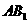 与
与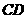 的公垂线;
的公垂线;
(Ⅱ)设异面直线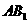 与
与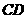 的夹角为45°,求二面角
的夹角为45°,求二面角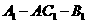 的大小.
的大小.
[分析]本题考查了立体几何中直线与平面、平面与平面及异面直线所成角与二面角的基础知识。
(1)要证明DE为AB1与CD的公垂线,即证明DE与它们都垂直,由AE=3EB1,有DE与BA1平行,由A1ABB1为正方形,可证得,证明CD与DE垂直,取AB中点F。连结DF、FC,证明DE与平面CFD垂直即可证明DE与CD垂直。
(2)由条件将异面直线AB1,CD所成角找出即为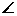 FDC,设出AB连长,求出所有能求出的边长,再作出二面角的平面角,根据所求的边长可通过解三角形求得。
FDC,设出AB连长,求出所有能求出的边长,再作出二面角的平面角,根据所求的边长可通过解三角形求得。
[解析]解法一: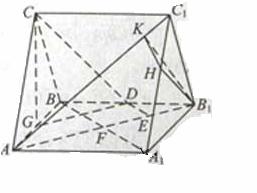 (Ⅰ)连结
(Ⅰ)连结 ,记
,记 与
与 的交点为F.因为面
的交点为F.因为面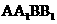 为正方形,故
为正方形,故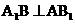 ,且
,且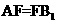 .又
.又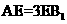 ,所以
,所以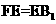 ,又D为
,又D为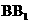 的中点,故
的中点,故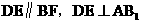 .
.
作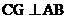 ,G为垂足,由AC=BC知,G为AB中点.
,G为垂足,由AC=BC知,G为AB中点.
又由底面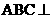 面
面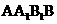 ,得
,得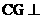
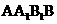 .
.
连结DG,则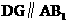 ,故
,故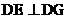 ,由三垂线定理,得
,由三垂线定理,得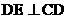 .
.
所以DE为异面直线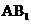 与CD的公垂线.
与CD的公垂线.
(Ⅱ)因为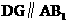 ,故
,故 为异面直线
为异面直线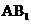 与
与 的夹角,
的夹角,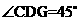 .
.
设AB=2,则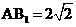 ,
,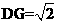 ,
,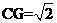 ,
, .
.
作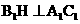 ,H为垂足,因为底面
,H为垂足,因为底面 ,故
,故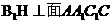 ,
,
又作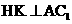 ,K为垂足,连结
,K为垂足,连结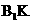 ,由三垂线定理,得
,由三垂线定理,得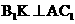 ,因此
,因此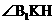 为
为
解法二:(Ⅰ)以B为坐标原点,射线BA为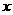 轴正半轴,建立如图所示的空间直角坐标系
轴正半轴,建立如图所示的空间直角坐标系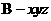 .设AB=2,则A(2,0,0,),
.设AB=2,则A(2,0,0,),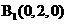 ,D(0,1,0),
,D(0,1,0),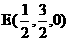 ,
,
又设C(1,0,c),则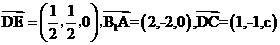 .
.
于是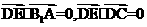 .
.
故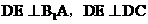 ,
,
 所以DE为异面直线
所以DE为异面直线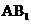 与CD的公垂线.
与CD的公垂线.
(Ⅱ)因为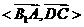 等于异面直线
等于异面直线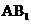 与CD的夹角,
与CD的夹角,
故  ,
,
即 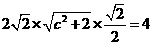 ,
,
解得 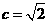 ,故
,故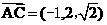 ,
,
又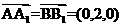 ,
,
所以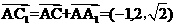 ,
,

所以 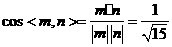 .
.
由于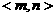 等于二面角
等于二面角 的平面角,
的平面角,
所以二面角 的大小为
的大小为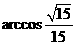 .
.
20.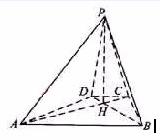 (全国Ⅰ新卷文18)如图,已知四棱锥
(全国Ⅰ新卷文18)如图,已知四棱锥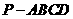 的底面为等腰梯形,
的底面为等腰梯形,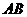 ∥
∥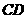 ,
,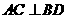 ,垂足为
,垂足为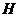 ,
,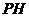 是四棱锥的高。
是四棱锥的高。
(Ⅰ)证明:平面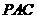
 平面
平面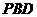 ;
;
(Ⅱ)若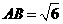 ,
,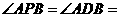 60°,求四棱锥
60°,求四棱锥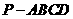 的体积。
的体积。
解: (1)因为PH是四棱锥P-ABCD的高。
所以AC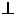 PH,又AC
PH,又AC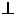 BD,PH,BD都在平PHD内,且PH
BD,PH,BD都在平PHD内,且PH BD=H.
BD=H.
所以AC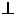 平面PBD.
平面PBD.
故平面PAC平面PBD. ……..6分
(2)因为ABCD为等腰梯形,AB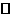 CD,AC
CD,AC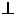 BD,AB=
BD,AB=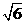 .
.
所以HA=HB=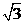 .
.
因为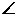 APB=
APB=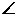 ADR=600
ADR=600
所以PA=PB=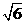 ,HD=HC=1.
,HD=HC=1.
可得PH=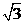 .
.
等腰梯形ABCD的面积为S=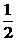 AC
x BD = 2+
AC
x BD = 2+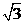 . ……..9分
. ……..9分
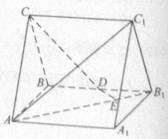 所以四棱锥的体积为V=
所以四棱锥的体积为V=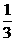 x(2+
x(2+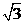 )x
)x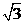 =
=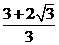 ……..12分
……..12分
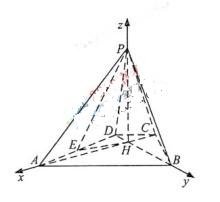
19.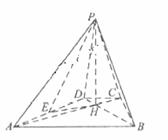 (全国Ⅰ新卷理18)如图,已知四棱锥P-ABCD的底面为等腰梯形,AB
(全国Ⅰ新卷理18)如图,已知四棱锥P-ABCD的底面为等腰梯形,AB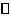 CD,AC
CD,AC BD,垂足为H,PH是四棱锥的高 ,E为AD中点
BD,垂足为H,PH是四棱锥的高 ,E为AD中点
证明:PE BC
BC
若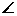 APB=
APB= ADB=60°,求直线PA与平面PEH所成角的正弦值
ADB=60°,求直线PA与平面PEH所成角的正弦值
解:
 以
以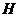 为原点,
为原点,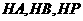 分别为
分别为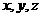 轴,线段
轴,线段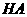 的长为单位长,
建立空间直角坐标系如图, 则
的长为单位长,
建立空间直角坐标系如图, 则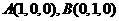
(Ⅰ)设 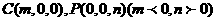
则 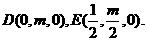
可得 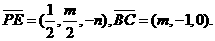
因为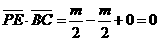
所以 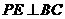
(Ⅱ)由已知条件可得
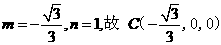
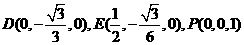 设
设 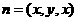 为平面
为平面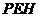 的法向量
的法向量
则 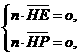 即
即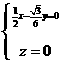 因此可以取
因此可以取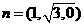 ,
,
由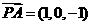 ,可得
,可得 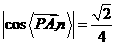
所以直线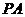 与平面
与平面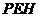 所成角的正弦值为
所成角的正弦值为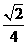
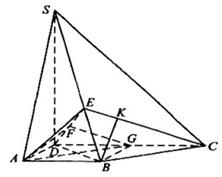
18.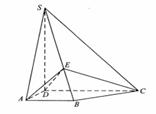 (全国Ⅰ卷理19文20)如图,四棱锥S-ABCD中,SD
(全国Ⅰ卷理19文20)如图,四棱锥S-ABCD中,SD 底面ABCD,AB//DC,AD
底面ABCD,AB//DC,AD DC,AB=AD=1,DC=SD=2,E为棱SB上的一点,平面EDC
DC,AB=AD=1,DC=SD=2,E为棱SB上的一点,平面EDC 平面SBC .
平面SBC .
(Ⅰ)证明:SE=2EB;
(Ⅱ)求二面角A-DE-C的大小 .
[解析]解法一:
(Ⅰ)连接BD,取DC的中点G,连接BG,
由此知 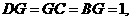 即
即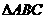 为直角三角形,故
为直角三角形,故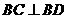 .
.
又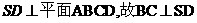 ,
,
所以,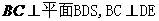 .
.
 作
作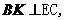
 ,
,

(Ⅱ) 由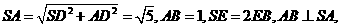 知
知
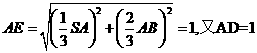 .
.
故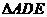 为等腰三角形.
为等腰三角形.
取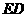 中点F,连接
中点F,连接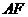 ,则
,则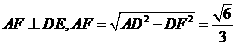 .
.
连接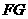 ,则
,则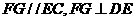 .
.
所以,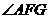 是二面角
是二面角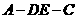 的平面角.
的平面角.
连接AG,AG= ,
,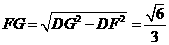 ,
,
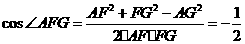 ,
,
所以,二面角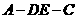 的大小为120°.
的大小为120°.
解法二: 以D为坐标原点,射线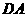 为
为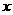 轴的正半轴,建立如图所示的直角坐标系
轴的正半轴,建立如图所示的直角坐标系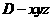 ,
,

由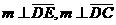 ,得
,得
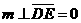 ,
,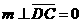
故
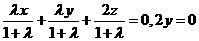 .
.
令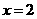 ,则
,则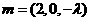 .
.

17. (辽宁卷文19)如图,棱柱
(辽宁卷文19)如图,棱柱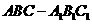 的侧面
的侧面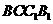 是菱形,
是菱形,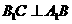
(Ⅰ)证明:平面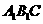
 平面
平面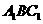 ;
;
(Ⅱ)设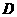 是
是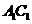 上的点,且
上的点,且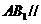 平面
平面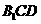 ,求
,求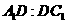 的值。
的值。
解:(Ⅰ)因为侧面BCC1B1是菱形,所以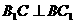
又已知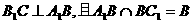
所又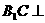 平面A1BC1,又
平面A1BC1,又 平面AB1C ,
平面AB1C ,
所以平面 平面A1BC1 .
平面A1BC1 .
(Ⅱ)设BC1交B1C于点E,连结DE, 则DE是平面A1BC1与平面B1CD的交线,
因为A1B//平面B1CD,所以A1B//DE.
又E是BC1的中点,所以D为A1C1的中点.即A1D:DC1=1.
[命题意图]本小题主要考查空间直线与直线、直线与平面、平面与平面的位置关系,二面角等基础知识,考查空间想象能力、推理论证能力和运算能力.
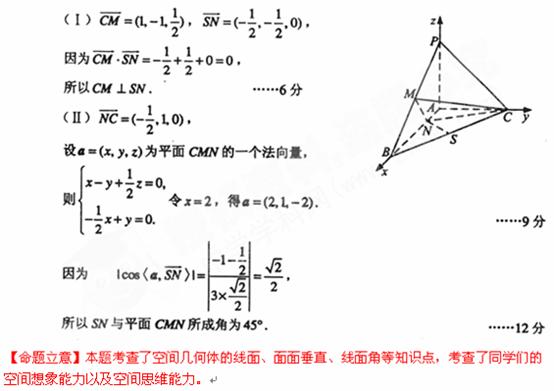
16.(辽宁卷理19)已知三棱锥P-ABC中,PA⊥ABC,AB⊥AC,PA=AC=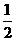 AB,N为AB上一点,AB=4AN,M,S分别为PB,BC的中点.
AB,N为AB上一点,AB=4AN,M,S分别为PB,BC的中点.
(Ⅰ)证明:CM⊥SN;
(Ⅱ)求SN与平面CMN所成角的大小.

[点评]纵观近几年的高考试题,立体几何的解答题在很大程度上扮演着直线与平面内容载体的角色,着重考查立体几何中的逻辑推理,多为中档题,通过这些题目考查学生掌握基础知识、逻辑推理能力、计算能力和空间想象能力。而空间向量是解答立体几何问题的
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com