21. (本小题满分13分)

已知数列{a_n}的前n项和为S_n，S_n=2-(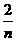+1)a_n(n≥1)．

(1)求证：数列{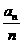}是等比数列；

(2)设数列{2ⁿa_n}的前n项和为T_n，A_n=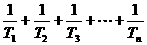.试比较A_n与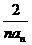的大小。

20. (本小题满分13分)

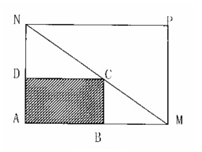某建筑工地在一块长AM=30米，宽AN=20米的矩形地块AMPN上施工，规划建设占地如图中矩形ABCD的学生公寓，要求顶点C在地块的对角线MN上，B，D分别在边AM，AN上，假设AB长度为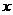米。

　 (1)要使矩形学生公寓ABCD的面积不小于144平方米，

AB的长度应在什么范围？

　 (2)长度AB和宽度AD分别为多少米时矩形学生公寓

ABCD的面积最大？最大值是多少平方米？

19. (本小题满分12分)

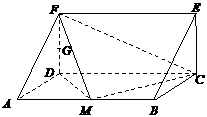如图，在三棱柱ADF-BCE中，侧棱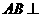底面，底面是等腰直角三角形，且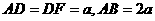，M、G分别是AB、DF的中点.

(1)求证GA∥平面FMC;

(2)求直线DM与平面ABEF所成角。

18.　 (本小题满分12分)

盒中有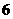个小球,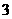个白球,记为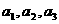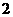，个红球, 记为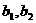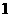，个黑球, 记为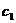，除了颜色和编号外,球没有任何区别.

　　 (1) 求从盒中取一球是红球的概率；

　　 (2) 从盒中取一球，记下颜色后放回，再取一球，记下颜色，若取白球得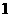分，取

红球得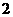分，取黑球得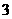分，求两次取球得分之和为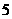分的概率.[

17. (本小题满分12分)

已知函数．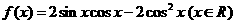

(1)求函数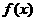的最小正周期；

(2)当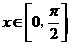时，求函数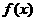的取值范围．

16．设直线参数方程为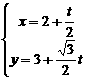(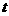为参数)，则它的斜截式方程为　　　　　

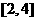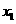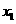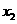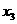15．用0.618法选取试点过程中，如果试验区间为，为第一个试点，且处的结果比处好，则为　　　　　　　

14. 在平面直角坐标系中，定义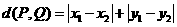为两点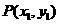,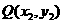之间的“折线距离”. 若点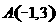，为坐标原点,则=　　　　　　　 ;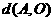

　　 与直线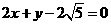上一点的“折线距离”的最小值是____；

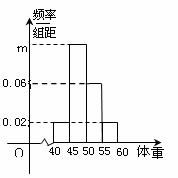
13. 从某校随机抽取名学生，将他们的体重

(单位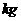：)数据绘制成频率分布直方图(如图)，

由图中数据可知=　　　　 ，所抽取的学生中

体重在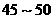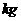的人数是　　　　 ．

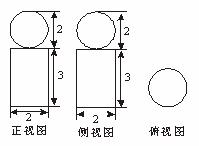
12. 如图是一个几何体的三视图，根据图中数据，

可得该几何体的表面积是