
题目列表(包括答案和解析)
(注意 :在试卷上作答无效)
:在试卷上作答无效)
(13)(1-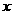 )20的二项展开式中,x
)20的二项展开式中,x 的系数与x9的系数之差为 .
的系数与x9的系数之差为 .
(14)已知a∈(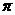 ,
,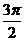 ),tanα=2,则cos2α= .
),tanα=2,则cos2α= .
(15)已知正方体ABCD-A1B1C1D1中,E为C1D1的中点,则异面直线AE与BC所成角的余弦值为
.
(16)已知F1、F2分别为双曲线C: 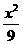 -
- 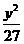 =1的左、右焦点,点A∈C,点M的坐标为(2,0),AM为∠F1AF2的平分线.则|AF2| = .
=1的左、右焦点,点A∈C,点M的坐标为(2,0),AM为∠F1AF2的平分线.则|AF2| = .
(1)设集合U=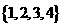 ,
,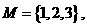
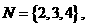 则
则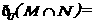
(A)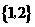 (B)
(B)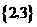 (C)
(C)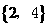 (D)
(D)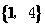
(2)函数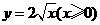 的反函数为
的反函数为
(A)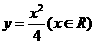 (B)
(B)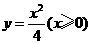
(C)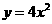
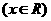 (D)
(D)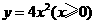
(3)设向量a,b满足|a|=|b|=1,则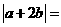
(A)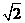 (B)
(B)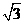 (C)
(C)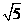 (D)
(D)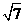
(4)若变量x,y满足约束条件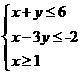 ,则
,则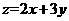 的最小值为
的最小值为
(A)17 (B)14 (C)5 (D)3
(5)下面四个条件中,使a>b成立的充分而不必要的条件是
(A) 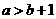 (B)
(B) 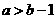 (C) a2> b2 (D) a3> b3
(C) a2> b2 (D) a3> b3
(6) 设Sn为等差数列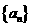 的前n项和,若a1=1,公差d=2,Sk+2-Sk=24,则k=
的前n项和,若a1=1,公差d=2,Sk+2-Sk=24,则k=
(A)8 (B)7 (C) 6 (D) 5
(7)设函数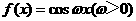 ,将
,将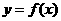 的图像向右平移
的图像向右平移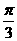 个单位长度后,所得的图像与原图像重合,则
个单位长度后,所得的图像与原图像重合,则 的最小值等于
的最小值等于
(A)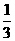 (B)
(B)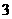 (C)
(C)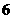 (D)
(D)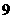
(8) 已知直二面角α- l –β,点A∈α,AC⊥l,C为垂足,点B∈β,BD⊥l,D为垂足.若AB=2,AC=BD=1,则CD=
(A) 2 (B)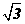 (C)
(C)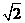 (D)1
(D)1
(9)4位同学每人从甲、乙、丙3门课程中选修1门,则恰有2人选修课程甲的不同选法共有
(A) 12种 (B) 24种 (C) 30种 (D)36种
(10)设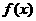 是周期为2的奇函数,当0≤x≤1时,
是周期为2的奇函数,当0≤x≤1时,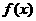 =
=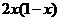 ,则
,则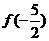 =
=
(A) -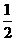 (B)
(B)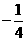 (C)
(C)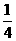 (D)
(D)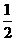
(11)设两圆 、
、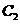 都和两坐标轴相切,且都过点(4,1),则两圆心的距离
都和两坐标轴相切,且都过点(4,1),则两圆心的距离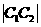 =
=
(A)4 (B)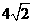 (C)8 (D)
(C)8 (D)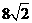
(12)已知平面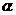
 截一球面得圆M , 过圆心M且与
截一球面得圆M , 过圆心M且与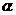 成
成 ,二面角的平面
,二面角的平面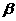 截该球面得圆N.若该球的半径为4,圆M的面积为4
截该球面得圆N.若该球的半径为4,圆M的面积为4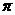 ,则圆N的面积为
,则圆N的面积为
(A)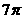 (B)
(B)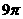 (c)
(c) (D)
(D)
第Ⅱ卷
1答题前,考生先在答题卡上用直径0.5毫米黑色墨水签字笔将自己的姓名、准考 证号填写清楚,然后贴好条形码。请认真核准条形码卜的准考证号、姓名和科目。2第Ⅱ卷共2页,请用直径0.5毫米黑色墨水签字笔在答题卡上各 题的答题区域
题的答题区域  内作答,在试题卷上作答无效。
内作答,在试题卷上作答无效。
3第Ⅱ卷共l0小题,共90分。
23.(本大题满分18分,第1小题满分4分,第二小题满分6分,第3小题满分8分)
已知平面上的线段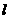 及点
及点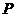 ,任取
,任取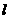 上一点
上一点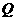 ,线段
,线段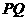 长度的最小值称为点
长度的最小值称为点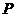 到线段
到线段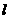 的距离,记作
的距离,记作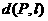
(1)求点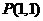 到线段
到线段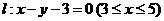 的距离
的距离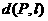 ;
;
(2)设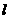 是长为2的线段,求点的集合
是长为2的线段,求点的集合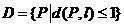 所表示的图形面积;
所表示的图形面积;
(3)写出到两条线段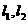 距离相等的点的集合
距离相等的点的集合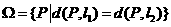 ,其中
,其中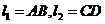 ,
,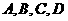 是下列三组点中的一组.
是下列三组点中的一组.
对于下列三种情形,只需选做一种,满分分别是①2分,② 6分,③8分;若选择了多于一种情形,则按照序号较小的解答
6分,③8分;若选择了多于一种情形,则按照序号较小的解答 计分.
计分.
① .
.
②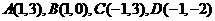 .
.
③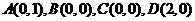 .
.
22.(本大题满分18 分,第1小题满分4分,第二小题满分6分,第3小题满分8分)
分,第1小题满分4分,第二小题满分6分,第3小题满分8分)
已知数列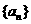 和
和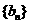 的通项公式分别为
的通项公式分别为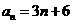 ,
,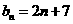
 (
(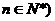 .将集合
.将集合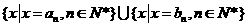 中的元素从小到大依次排列,构成数列
中的元素从小到大依次排列,构成数列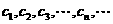
(1)写出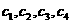 ;
;
(2)求证:在数列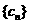 中,但不在数列
中,但不在数列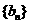 中的项恰为
中的项恰为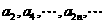 ;
;
(3)求数列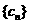 的通项公式.
的通项公式.
21. (本大题满分14分,第1小题满分6分,第二小题满分8分)
已知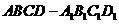 是底面边长为1的正四棱柱,
是底面边长为1的正四棱柱,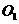 为
为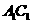 与
与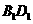 的交点.
的交点.
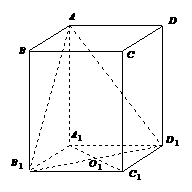 (1)设
(1)设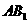 与底面
与底面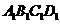 所成角的大小为
所成角的大小为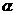 ,二面角
,二面角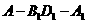 的大小为
的大小为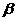 .求证:
.求证: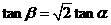 ;
;
(2)若点C到平面AB1D1的距离为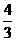 ,求正四棱柱
,求正四棱柱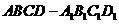 的高.
的高.
20.(本大题满分12分,第1小题满分4分,第二小题满分8分)
已知函数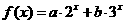 ,其中常数
,其中常数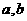 满足
满足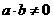
(1)若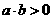 ,判断函数
,判断函数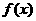 的单调性;
的单调性;
(2)若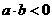 ,求
,求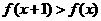 时的
时的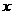 的取值范围.
的取值范围.
19.(本大题满分12分)
已知复数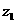 满足
满足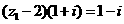 (
(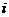 为虚数单位),复数
为虚数单位),复数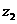 的虚部为2,且
的虚部为2,且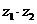 是实数,求
是实数,求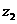 .
.
18.设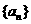 是各项为正数的无穷数列,
是各项为正数的无穷数列, 是边长为
是边长为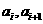 的矩形的面积(
的矩形的面积(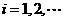 ),则
),则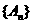 为等比数列的充要条件是( )
为等比数列的充要条件是( )
(A)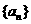 是等比数列.
是等比数列.
 (B)
(B)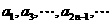 或
或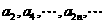 是等比数列.
是等比数列.
(C)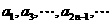 和
和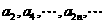 均是等比数列.
均是等比数列.
(D)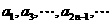 和
和
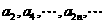 均是等比数列,且公比相同.
均是等比数列,且公比相同.
17. 设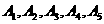 是平面上给定的5个不同点,则使
是平面上给定的5个不同点,则使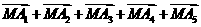
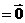 成立的点
成立的点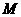 的个数为( )
的个数为( )
(A) .
(B)1.
(C)5.
(D)10.
.
(B)1.
(C)5.
(D)10.
16.下列函数中,既是偶函数,又是在区间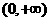 上单调递减的函数是( )
上单调递减的函数是( )
(A)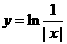 .
(B)
.
(B)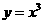 .
(C)
.
(C)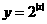 .
(D)
.
(D)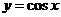 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com