2．生产一定数量的商品的全部费用称为生产成本，某企业一个月生产某种商品x万件时的生产成本为C(x)＝x²+2x+20(万元)．一万件售价是20万元，为获取更大利润，该企业一个月应生产该商品数量为(　)

A．36万件　 　　　　　　　　　　 B．18万件

C．22万件　 　　　　　　　　　　 D．9万件

解析：利润L(x)＝20x－C(x)＝－(x－18)²+142，当x＝18时，L(x)有最大值．

答案：B

1．某企业去年销售收入1000万元，年成本为生产成本500万元与年广告成本200万元两部分．若年利润必须按p%纳税，且年广告费超出年销售收入2%的部分也按p%纳税，其他不纳税．已知该企业去年共纳税120万元．则税率p%为(　)

A．10%　　　　　B．12%

C．25%　 　　　　　　　　　　　　 　D．40%

解析：利润300万元，纳税300·p%万元，

年广告费超出年销售收入2%的部分为

200－1000×2%＝180(万元)，

纳税180·p%万元，

共纳税300·p%+180·p%＝120(万元)，

p%＝＝25%.

答案：C

12．设有抛物线C：y＝－x²+x－4，过原点O作C的切线y＝kx，使切点P在第一象限．

(1)求k的值；

(2)过点P作切线的垂线，求它与抛物线的另一个交点Q的坐标．

解：(1)设点P的坐标为(x₁，y₁)，则y₁＝kx₁①

y₁＝－x+x₁－4②

①代入②得x+(k－)x₁+4＝0.

∵P为切点，

∴Δ＝(k－)²－16＝0得k＝或k＝.

当k＝时，x₁＝－2，y₁＝－17.

当k＝时，x₁＝2，y₁＝1.

∵P在第一象限，∴所求的斜率k＝.

(2)过P点作切线的垂线，其方程为y＝－2x+5③

将③代入抛物线方程得x²－x+9＝0.

设Q点的坐标为(x₂，y₂)，

即2x₂＝9，∴x₂＝，y₂＝－4.

∴Q点的坐标为(，－4)．

11．已知曲线y＝x²－1与y＝1+x³在x＝x₀处的切线互相垂直，求x₀的值．

解：对于y＝x²－1，有y′＝x，k₁＝y′|x＝x₀＝x₀；

对于y＝1+x³，有y′＝3x²，k₂＝y′|x＝x₀＝3x.

又k₁k₂＝－1，则x＝－1，x₀＝－1.

10．求下列函数的导数．

(1)y＝x²sinx；(2)y＝；

解：(1)y′＝(x²)′sinx+x²(sinx)′＝2xsinx+x²cosx.

(2)法一：y′＝

＝＝.

法二：∵y＝＝1+，

∴y′＝1′+′，即y′＝.

9．已知f₁(x)＝sinx+cosx，记f₂(x)＝f₁′(x)，f₃(x)＝f₂′(x)，…，f_n(x)＝f_n－1′(x)(n∈N^*，n≥2)，则f₁()+f₂()+…+f_{2 012}()＝________.

解析：f₂(x)＝f₁′(x)＝cosx－sinx，

f₃(x)＝(cosx－sinx)′＝－sinx－cosx，

f₄(x)＝－cosx+sinx，f₅(x)＝sinx+cosx，

以此类推，可得出f_n(x)＝f_n+4(x)

又∵f₁(x)+f₂(x)+f₃(x)+f₄(x)＝0，

∴f₁()+f₂()+…+f₂₀₁₂()＝f₁()+f₂()+f₃()+f₄()＝0.

答案：0

8．在平面直角坐标系xOy中，点P在曲线C：y＝x³－10x+3上，且在第二象限内，已知曲线C在点P处的切线的斜率为2，则点P的坐标为________．

解析：∵y＝x³－10x+3，∴y′＝3x²－10.

由题意，设切点P的横坐标为x₀，且x₀<0，

即3x－10＝2，∴x＝4，∴x₀＝－2，

∴y₀＝x－10x₀+3＝15.

故点P的坐标为(－2,15)．

答案：(－2,15)

7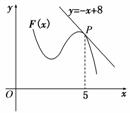．如图，函数F(x)＝f(x)+x²的图象在点P处的切线方程是y＝－x+8，则f(5)+f′(5)＝______.

解析：F′(x)＝f′(x)+x，

由题意可知F′(5)＝f′(5)+2＝－1，

∴f′(5)＝－3.

又点(5,3)在F(x)上，∴f(5)+5＝3，

∴f(5)＝－2，∴f(5)+f′(5)＝－5.

答案：－5

6．f(x)与g(x)是定义在R上的两个可导函数，若f(x)，g(x)满足f′(x)＝g′(x)，则f(x)与g(x)满足(　)

A．f(x)＝g(x)　 B．f(x)＝g(x)＝0

C．f(x)－g(x)为常数函数　 D．f(x)+g(x)为常数函数

解析：由f′(x)＝g′(x)，得f′(x)－g′(x)＝0，

即[f(x)－g(x)]′＝0，所以f(x)－g(x)＝C(C为常数)．

答案：C

5．若函数f(x)＝e^xcosx，则此函数图象在点(1，f(1))处的切线的倾斜角为(　)

A．0　 　　　　　　　　　　　　 B．锐角

C．直角　 　　　　　　　　　 D．钝角

解析：由已知得：

f′(x)＝e^xcosx－e^xsinx＝e^x(cosx－sinx)．

∴f′(1)＝e(cos1－sin1)．

∵>1>.

而由正余弦函数性质可得cos1<sin1.

∴f′(1)<0.

即f(x)在(1，f(1))处的切线的斜率k<0.

∴切线倾斜角是钝角．

答案：D