
题目列表(包括答案和解析)
3. 注重应用意识的培养
注重培养用数学的眼光观察和分析实际问题,提高数学的兴趣,增强学好数学的信心,达到培养创新精神和实践能力的目的。
1. 审题观 2. 思想方法观 3. 步骤清晰、层次分明观
2.注重思维的严谨性
平时学习过程中应避免只停留在“懂”上,因为听懂了不一定会,会了不一定对,对了不一定美。即数学学习的五种境界:听--懂--会--对--美。
我们今后要在第五种境界上下功夫,每年的高考结束,结果下来都可以发现我们宿迁市的考生与南方的差距较大,这就是其中的一个原因。
另外我们的学生的解题的素养不够,比如仅仅一点“规范答题”问题,我们老师也强调很多遍,但作为学生的你们又有几人能够听进去!
希望大家还是能够做到我经常所讲的做题的“三观” :
1. 注重基础和通性通法
在平时的学习中,应立足教材,学好用好教材,深入地钻研教材,挖掘教材的潜力,注意避免眼高手低,偏重难题,搞题海战术,轻视基础知识和基本方法的不良倾向,当然注重基础和通性通法的同时,应注重一题多解的探索,经常利用变式训练和变式引申来提高自己的分析问题、解决问题的能力。
7.已知二次函数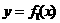 的图象以原点为顶点且过点(1,1),反比例函数
的图象以原点为顶点且过点(1,1),反比例函数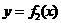 的图象与直线
的图象与直线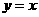 的两个交点间的距离为8,
的两个交点间的距离为8,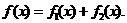
(1)求函数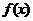 的表达式;
的表达式;
(2)证明:当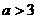 时,关于
时,关于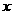 的方程
的方程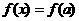 有三个实数解.
有三个实数解.
解析:(1)由已知,设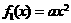 ,由
,由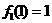 ,得
,得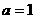 ,∴
,∴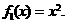
设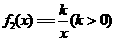 ,它的图象与直线
,它的图象与直线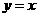 的交点分别为
的交点分别为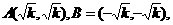
由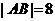 ,得
,得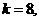
∴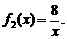 故
故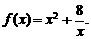
(2)证明:由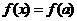 ,得
,得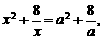
 即
即 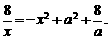
在同一坐标系内作出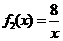 和
和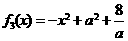 的大致图象如图,其中
的大致图象如图,其中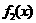 的图象是以坐标轴为渐近线,且位于第一、三象限的双曲线,
的图象是以坐标轴为渐近线,且位于第一、三象限的双曲线,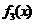 的图象是以
的图象是以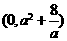 为顶点,开口向下的抛物线.
为顶点,开口向下的抛物线.
∴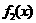 与
与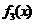 的图象在第三象限有一个交点,
的图象在第三象限有一个交点,
即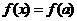 有一个负数解.
有一个负数解.
又∵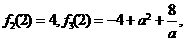
当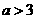 时,
时,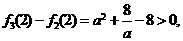
∴当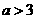 时,在第一象限
时,在第一象限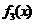 的图象上存在一点
的图象上存在一点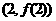 在
在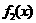 图象的上方.
图象的上方.
∴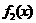 与
与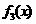 的图象在第一象限有两个交点,
的图象在第一象限有两个交点,
即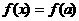 有两个正数解.
有两个正数解.
∴方程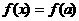 有三个实数解.
有三个实数解.
6.方程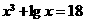 的根
的根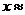 。(结果精确到0.1)
。(结果精确到0.1)
[解析]令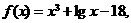
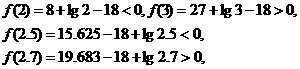
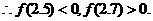 取
取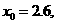
∵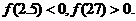 取
取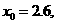
∵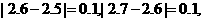
∴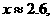
∵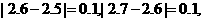
∴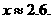
故应填:2.6.
5.二次函数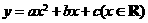 的部分对应值如下表:
的部分对应值如下表:
 |
 |
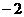 |
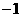 |
0 |
1 |
2 |
3 |
4 |
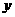 |
6 |
0 |
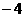 |
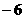 |
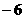 |
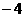 |
0 |
6 |
则使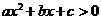 成立的自变量
成立的自变量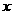 的取值范围是
。
的取值范围是
。
[解析]由表中数据可知 ,因此函数的零点有两个是
,因此函数的零点有两个是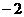 和3,这两个零点将
和3,这两个零点将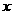 轴分成三个区间
轴分成三个区间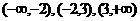 .在区间
.在区间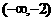 中取特殊值
中取特殊值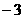 ,表中数据有
,表中数据有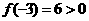 ,因此根据二次函数零点的性质得:当
,因此根据二次函数零点的性质得:当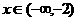 时,都有
时,都有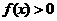 ;同理可得:当
;同理可得:当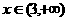 时也有
时也有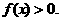 故使
故使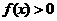 的自变量
的自变量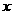 的取值范围是
的取值范围是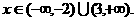
故应填:
4.三次方程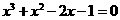 在下列哪些连续整数之间有根?( )
在下列哪些连续整数之间有根?( )
A.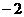 与
与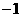 之间 B.
之间 B.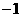 与0之间 C.0与1之间
与0之间 C.0与1之间
D.1与2之间 E.2与3之间
[解析]令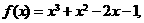
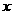 |
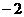 |
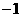 |
0 |
1 |
2 |
3 |
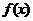 |
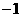 |
1 |
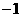 |
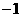 |
7 |
29 |
根据勘根定理:
∵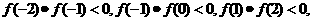
∴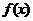 在
在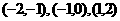 内均有根。
内均有根。
∴选A、B、D.
3.设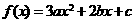 ,若
,若 ,求证:
,求证:
(1)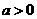 且
且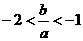 ;
;
(2)方程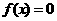 在
在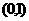 内有两个实数。
内有两个实数。
[解析](1)因为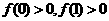 ,
,
所以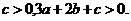
由条件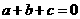 ,消去
,消去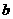 ,得
,得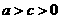 ;
;
由条件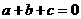 ,消去
,消去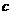 ,得
,得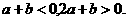
故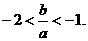
(2)抛物线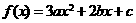 的顶点坐标为
的顶点坐标为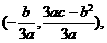
在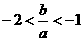 的两边乘以
的两边乘以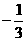 ,得
,得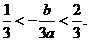
又因为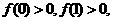 而
而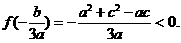
所以方程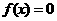 在区间
在区间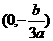 与
与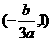 内分别有一实根。
内分别有一实根。
故方程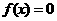 在
在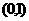 内有两个实根。
内有两个实根。
2.(理)已知函数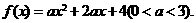 若
若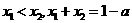 ,则( )
,则( )
A.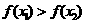 B.
B.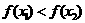
C.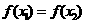 D.
D.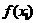 与
与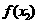 的大小不能确定
的大小不能确定
(文)已知函数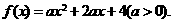 若
若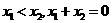 ,则( )
,则( )
A.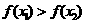 B.
B.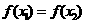
C.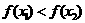 D.
D.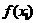 与
与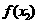 的大小不能确定
的大小不能确定
 [解析](理)
[解析](理)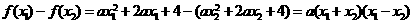
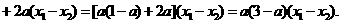
又∵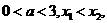
∴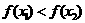 ,故选B。
,故选B。
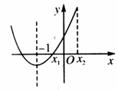
(文)由题意分析知二次函数的对称轴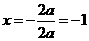 ,又
,又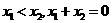 ,
,
∴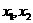 关于原点对称,结合图象分析知:
关于原点对称,结合图象分析知: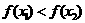 ,故选C。
,故选C。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com