
题目列表(包括答案和解析)
18.(本小题满分10分)
某工厂在试验阶段大量生产一种零件.这种零件有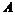 、
、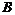 两项技术指标需要检测,设两项技术指标达标与否互不影响.若有且仅有一项技术指标达标的概率为
两项技术指标需要检测,设两项技术指标达标与否互不影响.若有且仅有一项技术指标达标的概率为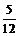 ,至少一项技术指标达标的概率为
,至少一项技术指标达标的概率为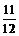 .按质量检验规定:两项技术指标都达标的零件为合格品.
.按质量检验规定:两项技术指标都达标的零件为合格品.
(1)求一个零件经过检测为合格品的概率是多少?
(2)任意依次抽出4个零件进行检测,设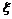 表示其中合格品的个数.
表示其中合格品的个数.
① 求其中至多2个零件是合格品的概率是多少?
② 求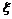 的均值
的均值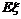 和方差
和方差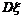 .
.
19 (本小题满分10分)
如图,已知三棱锥A – BCD的侧视图,俯视图都是直角三角形, 尺寸如图所示.
(1)求异面直线AB与CD所成角的余弦值;
(2)在线段AC上是否存在点F,使得BF⊥面ACD?若存在,求出CF的长度;若不存在说明理由.
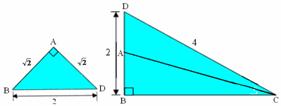 (侧视图) (俯视图) |
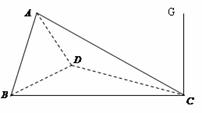 (第19题 ) |
17.如图,对正方体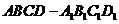 ,给出下列四个命题:
,给出下列四个命题:
① 在直线
在直线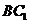 上运动时,三棱锥
上运动时,三棱锥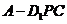 的体积不变;
的体积不变;
②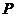 在直线
在直线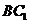 上运动时,直线AP与平面ACD1所成角的大小不变;
上运动时,直线AP与平面ACD1所成角的大小不变;
③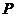 在直线
在直线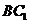 上运动时,二面角
上运动时,二面角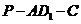 的大小不变;
的大小不变;
④M是平面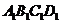 上到点D和
上到点D和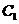 距离相等的点,则M点的轨迹与直线B1C1相交.
距离相等的点,则M点的轨迹与直线B1C1相交.
其中真命题的编号是 (写出所有真命题的编号).
16.已知 与
与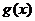 都是定义在R上的函数,
都是定义在R上的函数,
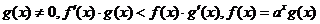
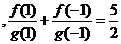 ,则在数列
,则在数列
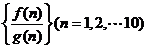 中,前
中,前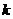 项和大于
项和大于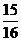 的概率是__ ___.
的概率是__ ___.
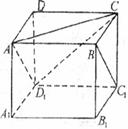 (第17题) |
15. 从装有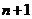 个球(其中
个球(其中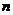 个白球,1个黑球)的口袋中取出
个白球,1个黑球)的口袋中取出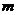 个球
个球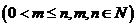 ,共有
,共有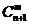 种取法,这
种取法,这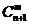 种取法可分成两类:一类是取出的
种取法可分成两类:一类是取出的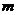 个球中,没有黑球, 有
个球中,没有黑球, 有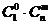 种取法,另一类是取出的
种取法,另一类是取出的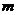 个球中有一个是黑球,有
个球中有一个是黑球,有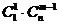 种取法,由此可得等式:
种取法,由此可得等式: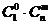 +
+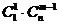 =
=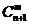 .则根据上述思想方法,当1£k<m<n,k, m, nÎN时,化简
.则根据上述思想方法,当1£k<m<n,k, m, nÎN时,化简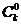 ·
·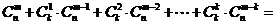 .
.
14.已知P是椭圆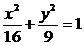 上的点,F1、F2分别是椭圆的左、右焦点,若∠F1PF2=60°,,则△F1PF2的面积为________
.
上的点,F1、F2分别是椭圆的左、右焦点,若∠F1PF2=60°,,则△F1PF2的面积为________
.
13.以椭圆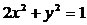 的顶点为焦点,以椭圆的焦点为顶点的双曲线方程为__ .
的顶点为焦点,以椭圆的焦点为顶点的双曲线方程为__ .
12.在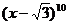 的展开式中,
的展开式中,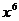 的系数是 .
的系数是 .
11.在空间直角坐标系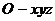 中,向量
中,向量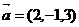 ,
,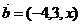 ,若
,若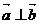 ,则
,则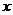 等于_____ ____.
等于_____ ____.
10.用4种不同的颜色为一个固定位置的正方体的六个面着色,要求相邻两个面颜色不相同,则不同的着色方法数是( )
A.24 B.48 C.72 D.96
9.若函数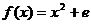 ,(e = 2.718…), 则下列命题正确的是( )
,(e = 2.718…), 则下列命题正确的是( )
A.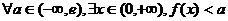 B.
B.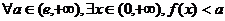
C.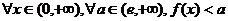 D.
D.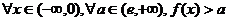
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com