
题目列表(包括答案和解析)
1. 过点M(2,1)作椭圆x2+4y2=16的弦AB,
(1) 若M是AB的中点,求弦AB所在的直线方程;[x+2y-4=0]
(2)
若|AM|=2|BM|,求弦AB所在的直线方程。[y= ]
]
6.
已知A,B分别是椭圆x2+4y2=4与圆x2+(y-2)2=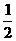 上的动点,求|AB的最大值。[
上的动点,求|AB的最大值。[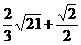 ]|
]|
5.
在曲线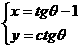 (q为参数)上求一点P,使它到直线x+2y+3=0的距离最小,并求出最小距离。[P(-
(q为参数)上求一点P,使它到直线x+2y+3=0的距离最小,并求出最小距离。[P(-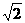 -1, -
-1, -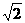 /2),2
/2),2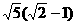 /5]
/5]
4. 证明:不论m为何值,双曲线x2-4y2-4mx+8(m+1)y-8m-84=0的两个焦点在两条平行直线上。
3.
已知曲线C的普通方程为y=1-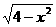 ,P(2,1)是曲线上的一点,Q(x,y)是曲线C上的点,弧长PQ的长为t,以t为参数,建立曲线C的参数方程。[
,P(2,1)是曲线上的一点,Q(x,y)是曲线C上的点,弧长PQ的长为t,以t为参数,建立曲线C的参数方程。[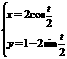 (t为参数0≤t≤2p)]
(t为参数0≤t≤2p)]
2.
分别在下列两种情况下,把参数方程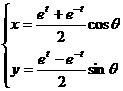 化为普通方程。
化为普通方程。
(1)q为参数,t为常数;(2)t为参数,q为常数。
1. 化下列方程为普通方程:
(1)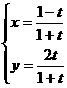 (t为参数)
[x+y-1=0(x≠-1)]
(t为参数)
[x+y-1=0(x≠-1)]
(2)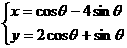 (q为参数)
[5x2+4xy+17y2=81]
(q为参数)
[5x2+4xy+17y2=81]
(3)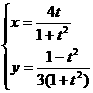 (t为参数)
[x2/4+9y2=1(y≠-1/3)]
(t为参数)
[x2/4+9y2=1(y≠-1/3)]
22、(本小题满分14分)
舰A在舰B的正东,距离6千米;舰C在舰B的北偏西300,距离4千米。它们准备围捕海中的一种动物。某时刻A发现动物信号,4秒后B、C同时发现这种信号。A向动物发射麻醉弹。假设舰与动物都是静止的,动物信号的传播速度为1千米/秒,炮弹初速度为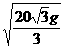 千米/秒,其中g为重力加速度,空气阻力不计,求舰A炮击的方位角与仰角。
千米/秒,其中g为重力加速度,空气阻力不计,求舰A炮击的方位角与仰角。
21、 (本小题满分14分)
(本小题满分14分)
定弓形弧上有一动点P,连接AP并延长至C,使∣AC∣=2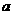 ;连接BP并
;连接BP并
延长至D,使∣BD∣=2b,求线段CD中点的轨迹方程。
20、(本小题满分12分)
建立极坐标系证明:已知半圆直径∣AB∣=2 (
( >0),半圆外一条直线
>0),半圆外一条直线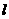 与AB所在直线垂直相交于点T,并且∣AT∣=2
与AB所在直线垂直相交于点T,并且∣AT∣=2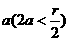 。若半圆上相异两点M、N到
。若半圆上相异两点M、N到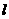 的距离∣MP∣,∣NQ∣满足∣MP∣∶∣MA∣=∣NQ∣∶∣NA∣=1,则 ∣MA∣+∣NA∣=∣AB∣。
的距离∣MP∣,∣NQ∣满足∣MP∣∶∣MA∣=∣NQ∣∶∣NA∣=1,则 ∣MA∣+∣NA∣=∣AB∣。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com