
题目列表(包括答案和解析)
13、沿某大街在甲、乙、丙三个地方设有红、绿灯交通信号,汽车在甲、乙、丙三个地方通过(即通过绿灯)的概率分别为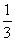 ,
,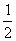 ,
,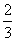 ,对于该大街上行驶的汽车,求:
,对于该大街上行驶的汽车,求:
(Ⅰ)在三个地方都不停车的概率;
(Ⅱ)在三个地方都停车的概率;
(Ⅲ)只在一个地方停车的概率.
解(1)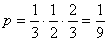 ;…………………………………………3分
;…………………………………………3分
(2)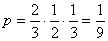 ; …………………………………………9分
; …………………………………………9分
(3)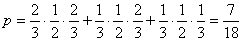 ………………………………………12分
………………………………………12分
12、某种电路开关闭合后,会出现红灯或绿灯闪动,已知开关第一次闭合后,出现红灯和出现绿灯的概率都是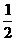 .从开关第二次闭合起,若前次出现红灯,则下一次出现红灯的概率是
.从开关第二次闭合起,若前次出现红灯,则下一次出现红灯的概率是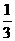 ,出现绿灯的概率是
,出现绿灯的概率是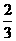 ;若前次出现绿灯,则下一次出现红灯的概率是
;若前次出现绿灯,则下一次出现红灯的概率是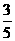 ,出现绿灯的概率是
,出现绿灯的概率是
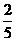 .问:
.问:
(Ⅰ)第二次闭合后出现红灯的概率是多少?
(Ⅱ)三次发光中,出现一次红灯、两次绿灯的概率是多少?
解(Ⅰ)如果第一次出现红灯,则接着又出现红灯的概率是 ;如果第一次出现绿灯,则接着出现红灯的概率为
;如果第一次出现绿灯,则接着出现红灯的概率为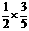 .………4分 综上,第二次出现红灯的概率为
.………4分 综上,第二次出现红灯的概率为 +
+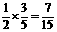 .……5分
.……5分
(Ⅱ)由题意,三次发光中,出现一次红灯、两次绿灯的情况共有如下三种方式:
①当出现绿、绿、红时的概率为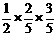 ;②当出现绿、红、绿时的概率为
;②当出现绿、红、绿时的概率为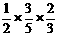 ;…9分
;…9分
③当出现红、绿、绿时的概率为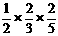 ;…………………………………………11分
;…………………………………………11分
所以三次发光中,出现一次红灯、两次绿灯的概率为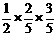 +
+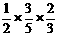 +
+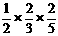 =
=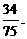 …12分
…12分
11、有一批种子,每粒发芽的概率为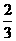 ,播下5粒种子,计算:
,播下5粒种子,计算:
(Ⅰ)其中恰好有4粒发芽的概率;
(Ⅱ)其中至少有4粒发芽的概率;
(Ⅲ)其中恰好有3粒没发芽的概率.
(以上各问结果均用最简分数作答)
解:(Ⅰ)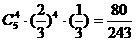
(Ⅱ)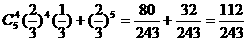
(Ⅲ)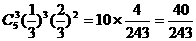
10、同时抛掷15枚均匀的硬币一次
(1)试求至多有1枚正面向上的概率;
(2)试问出现正面向上为奇数枚的概率与出现正面向上为偶数枚的概率是否相等?请说明理由.
解:(1)记“抛掷1枚硬币1次出现正面向上”为事件A,P(A)=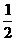 ,抛掷15枚硬币1次相当于作15次独立重复试验,根据几次独立重复试验中事件A发生K次的概率公式,记至多有一枚正面向上的概率为P1
,抛掷15枚硬币1次相当于作15次独立重复试验,根据几次独立重复试验中事件A发生K次的概率公式,记至多有一枚正面向上的概率为P1
则P1= P15(0)+ P15(1)=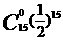 +
+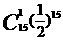 =
=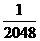 ……………(6分)
……………(6分)
(2)记正面向上为奇数枚的概率为P2,则有
P2= P15(1)+ P15(3)+…+ P15(15)=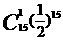 +
+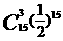 +…+
+…+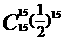
=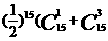 +…+
+…+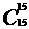 )–
)–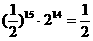 ………………………(10分)
………………………(10分)
又“出现正面向上为奇数枚”的事件与“出现正面向上为偶数枚” 的事件是对立事件,记“出现正面向上为偶数枚” 的事件的概率为P3
 P3=1–
P3=1–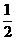 =
=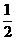
 相等
………………………(12分)
相等
………………………(12分)
9、一个电路中有三个电子元件,它们接通的概率都是m(0<m<1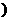 如图,有如下三
如图,有如下三
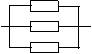 种联接方法:
种联接方法:
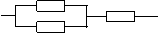
 ①
②
③
①
②
③
(1)分别求出这三种电路各自接通的概率;
(2)试分析这三种电路哪种性能最优,并证明你的结论.
解:三种电路各自接通分别记为事件A1、A2、A3,则P(A1)=m3…………3分
P(A2)=1-(1-m)3=3m-3m2+m3………6分 P(A3)=2(1-m)m2+m3=2m2-m3……9分
(2)P(A2)-P(A1)=3m-3m2=3m(1-m) ∵0<m<1 ∴P(A2)>P(A1)………10分
P(A2)-P(A3)=2m3-5m2+3m=m(2m-3)(m-1)>0 ∴P(A2)>P(A3)…………11分
三个电子元件并联接通的概率最大,故性能最优………………12分
8、在某次考试中,甲、乙、丙三人合格(互不影响)的概率分别是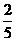 ,
,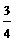 ,
,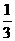 ,考试结束后,最容易出现几人合格的情况?
,考试结束后,最容易出现几人合格的情况?
解:按以下四种情况计算概率,概率最大的就是最容易出现的情况.
⑴三人都合格的概率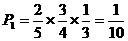 ………………………………………………2分
………………………………………………2分
⑵三人都不合格的概率为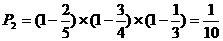 ……………………… 4分
……………………… 4分
⑶恰有两人合格的概率
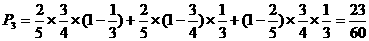 …………………………7分
…………………………7分
⑷恰有一人合格的概率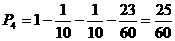 ………………………………… 10分
………………………………… 10分
由此可知,最容易出现恰有1人合格的情况……………………………………………12分
7. (Ⅰ)记“摸出两个球,两球恰好颜色不同”为A,
摸出两个球共有方法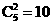 种, 其中,两球一白一黑有
种, 其中,两球一白一黑有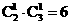 种. …………4分
种. …………4分
 .
………………………………6分
.
………………………………6分
(Ⅱ)法一:记摸出一球,放回后再摸出一个球 “两球恰好颜色不同”为B,
摸出一球得白球的概率为 ,摸出一球得黑球的概率为
,摸出一球得黑球的概率为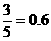 , ……8分
, ……8分
“有放回摸两次,颜色不同”指“先白再黑”或“先黑再白”, ……………10分
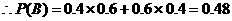 .
……………………………12分
.
……………………………12分
法二:有放回地摸两次,互相独立. 摸一次得白球的概率为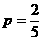 ,……10分
,……10分
 “有放回摸两次,颜色不同”的概率为
“有放回摸两次,颜色不同”的概率为
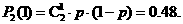 …………………………………………12分
…………………………………………12分
10、一个口袋中装有大小相同的2个白球和3个黑球.
(Ⅰ)从中摸出两个球,求两球恰好颜色不同的概率;
(Ⅱ)从中摸出一个球,放回后再摸出一个球,求两球恰好颜色不同的概率.
9、为了测试甲、乙两名篮球运动员投定位球的水平,在罚球线上让他们各投篮10次,甲投中7次,乙投中6次,如果让甲、乙依照各自的水平再投篮3次,求:
①甲运动员恰好投中2次的概率是什么?
②两名运动员都恰好投中2次的概率是多少?(结果保留两个有效数学)
解:设事件A:甲运动员投篮1次,投中 . 事件B:乙运动员投篮1次,投中 .
∴P(A)=0.7 , P(B)=0.6 ①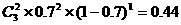 …………6分
…………6分
②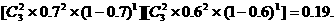 …………12分
…………12分
8、设在一袋子内装有5只白球,5只黑球,从这袋子内任意取球5次,每次取一只,每次取出的球又立即放回袋子中,求在这5次取球中(结果保留两个有效数学)
①取得白球3次的概率;
②至少有1次取得白球的概率
解:记“取球一次得白球”为事件A,“取球一次得黑球”为事件B.
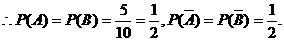 ①
①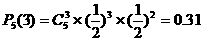 …6分
…6分
②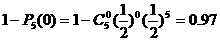
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com