
题目列表(包括答案和解析)
21.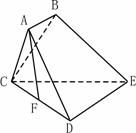 (12分)如图,已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,三角形ACD是正三角形且AD=DE=2,AB=1,F是CD的中点。
(12分)如图,已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,三角形ACD是正三角形且AD=DE=2,AB=1,F是CD的中点。
(1)求证:AF//平面BCE
(2)求二面角C-BE-D的正切值。
20.(12分)如图,在正三棱柱ABC-A1B1C1中,A1A=AB=a,G、E、F分别是A1C1、AB和BC的中点。
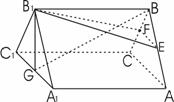 (1)(文科作)求证:EF⊥平面GB1B;
(1)(文科作)求证:EF⊥平面GB1B;
(理科作)求证:平面B1EF⊥平面GB1B;
(2)求点G到平面B1EF的距离。
19.(12分)某中学三个年级各有十个编号从1到10的班级,为探索教书育人新方法,在全校学生中实施以“立志、立法、立德”为内容的“三立”教育工程。为此在三个年级中抽取14名学生组成第一期“三立”教育指导培训班,要求每个班级至多有一名学生参加,抽取方法是:高一任意抽取8名学生;高二按班级序号的奇偶性分两组各抽取二名;高三抽取2名学生且所抽的班级序号不得相邻,则培训班共有多少种不同的组成方案?
若指派五名教师到三个年级指导“三立”工程实施,要求每个年级至少一人,则有多少种不同的分配方案?
18.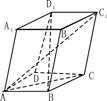 (12分)已知平行六面体ABCD-A1B1C1D1中,底面ABCD是边长为2且∠BAD=60°的菱形,∠A1AB=A1AD=45°,AA1=
(12分)已知平行六面体ABCD-A1B1C1D1中,底面ABCD是边长为2且∠BAD=60°的菱形,∠A1AB=A1AD=45°,AA1=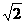
(1)求对角线AC1的长
(2)直线BD1与AC夹角的余弦值
17. (12分)已知∠BOC在平面
(12分)已知∠BOC在平面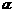 内,OA是平面
内,OA是平面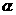 的斜线,∠AOB=∠AOC=60°,且OA=OB=OC=a,BC=
的斜线,∠AOB=∠AOC=60°,且OA=OB=OC=a,BC=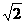 a,求OA与平面
a,求OA与平面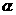 所成的角。
所成的角。
16.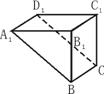 已知在长方体ABCD-A1B1C1D1中,A1B1=B1B=2,A1D1=1,沿该长方体的对角面A1D1CB切得一个几何体(如图),点P在△A1B1B面上运动,若点P到面B1C1CB的距离等于点P到棱A1D1的距离的
已知在长方体ABCD-A1B1C1D1中,A1B1=B1B=2,A1D1=1,沿该长方体的对角面A1D1CB切得一个几何体(如图),点P在△A1B1B面上运动,若点P到面B1C1CB的距离等于点P到棱A1D1的距离的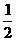 倍,则点P到点B1的距离的最小值是
。
倍,则点P到点B1的距离的最小值是
。
15.(文科)长方体的一个顶点上的三条棱分别是3,4,5,且它的八个顶点都在同一个球面上,这个球的表面积是 。
(理科)三棱锥A-BCD三个侧面两两垂直,底面BCD上一点P到三个侧面的距离分别为2,3,6,则P点到三棱锥顶点A的距离为 。
14.考察下列三个命题,在“
”处都缺少一个条件,补上这个条件使其构成真命题(其中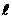 、m为直线,
、m为直线,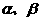 为平面)则此条件为 。
为平面)则此条件为 。


 ①
①
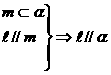 ②
②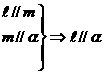 ③
③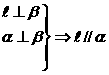
13.某乒乓球队共有男女队员18人,现从中选出男女队员各一人组成一对双打组合,由于在男队员中有两人主攻单打项目,不参与双打组合,这样一共有64种组合方式,则乒乓球队中女队员的人数为 人。
12.将一个四棱锥的每个顶点染上一种颜色,并使一条棱的两端异色,若只有4种颜色可供使用,则不同的染色方法种数为( )种
A.24 B.48 C. 60 D. 72
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com