
题目列表(包括答案和解析)
3.某人射击一次命中目标的概率是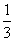 ,则此人射击
,则此人射击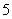 次,有
次,有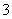 次命中目标且恰有两次连续命中的概率是
(
次命中目标且恰有两次连续命中的概率是
(  )
)
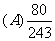
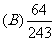
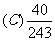
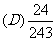
2.某校高三年级举行一次演讲比赛,共有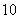 位同学参赛,其中一班有
位同学参赛,其中一班有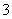 位,二班有
位,二班有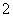 位,其他班级有
位,其他班级有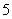 位。若采取抽签的方式确定他们的演讲顺序,则一班的
位。若采取抽签的方式确定他们的演讲顺序,则一班的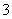 位同学没有被排在一起,而二班的
位同学没有被排在一起,而二班的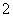 位同学恰好被排在一起(指演讲的序号相连)的概率是 (
位同学恰好被排在一起(指演讲的序号相连)的概率是 ( 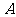 )
)
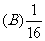
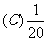
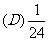
1.某工厂生产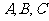 三种不同型号的产品,产品数量之比依次为
三种不同型号的产品,产品数量之比依次为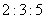 。现用分层抽样方法抽出一个容量为
。现用分层抽样方法抽出一个容量为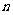 的样本,样本中
的样本,样本中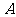 型号产品有
型号产品有 件,则此样本的容量为
(
件,则此样本的容量为
(  )
)
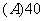
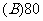
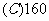
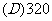
2.知识重点:
等可能事件的定义及其概率公式,互斥事件的定义及其概率的加法公式,相互独立事件的定义及其概率的乘法公式,独立重复试验的定义及其概率公式。互斥事件的概率加法公式对应着分类相加计数原理的应用,相互独立事件的概率乘法公式对应着分步相乘计数原理的应用。
[例题分析]
例1、 从数字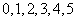 中,随机抽取
中,随机抽取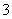 个数字(允许重复)组成一个三位数,其各位数字之和等于
个数字(允许重复)组成一个三位数,其各位数字之和等于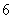 的概率为多少?
的概率为多少?
[思路分析] 本题的基本事件是由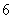 个不同的数字允许重复而且含
个不同的数字允许重复而且含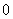 的条件下组成三位数,根据乘法原理可知基本事件的全体共有
的条件下组成三位数,根据乘法原理可知基本事件的全体共有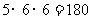 个。设三个数字之和等于
个。设三个数字之和等于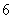 的事件为
的事件为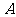 ,则
,则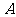 分为六类:数码
分为六类:数码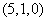 组成不同的三位数有
组成不同的三位数有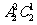 个;数码
个;数码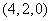 组成不同的三位数有
组成不同的三位数有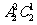 个;数码
个;数码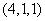 组成不同的三位数有
组成不同的三位数有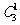 个;数码
个;数码 组成不同的三位数有
组成不同的三位数有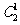 个;数码
个;数码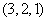 组成不同的三位数有
组成不同的三位数有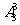 个;数码
个;数码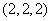 组成不同的三位数有
组成不同的三位数有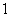 个,根据加法原理,事件
个,根据加法原理,事件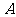 共有
共有
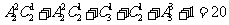 个。故
个。故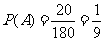 。
。
[简要评述] 本题考查等可能性事件的概率和互斥事件的概率,重点在于利用排列组合知识求各个基本事件的总数。
例2、鱼塘中共有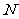 条鱼,从中捕得
条鱼,从中捕得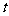 条,加上标志后立即放回塘中,经过一段时间,再从塘中捕出
条,加上标志后立即放回塘中,经过一段时间,再从塘中捕出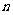 条鱼,发现其中有
条鱼,发现其中有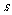 条标志鱼。
条标志鱼。
(1)问其中有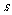 条标志鱼的概率是多少?(2)由此可推测塘中共有多少条鱼(即用
条标志鱼的概率是多少?(2)由此可推测塘中共有多少条鱼(即用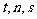 表示
表示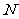 )?
)?
[思路分析] (1)由题意可知,基本事件总数为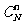 。鱼塘中的鱼分为两类:有标志的鱼
。鱼塘中的鱼分为两类:有标志的鱼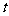 条,无标志的鱼
条,无标志的鱼 条,从而在捕出
条,从而在捕出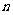 条鱼中,有标志的
条鱼中,有标志的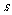 条鱼有
条鱼有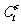 种可能,同时无标志的
种可能,同时无标志的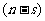 条鱼有
条鱼有 种可能,则捕出
种可能,则捕出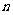 条鱼中有
条鱼中有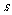 条鱼共有
条鱼共有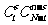 种可能。所以概率为
种可能。所以概率为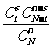 。
。
(2)由分层抽样可知,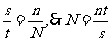 (条)。
(条)。
[简要评述] 本题考查等可能性事件的概率和统计知识,重点要注意“鱼”的不同的分类以及抽样方法中各个元素被抽取概率的相等性。
例3、某宾馆有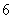 间客房,现要安排
间客房,现要安排 位旅游者,每人可以进住任意一个房间,且进住各房间是等可能的,求下列事件各的概率:(1)事件
位旅游者,每人可以进住任意一个房间,且进住各房间是等可能的,求下列事件各的概率:(1)事件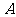 :指定的
:指定的 个房间各有
个房间各有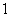 人;(2)事件
人;(2)事件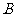 :恰有
:恰有 个房间各有
个房间各有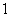 人;(3)事件
人;(3)事件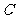 :指定的某房间中有
:指定的某房间中有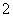 人;(4)事件
人;(4)事件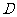 :一号房间有
:一号房间有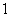 人,二号房间有
人,二号房间有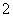 人;(5)事件
人;(5)事件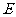 :至少有
:至少有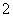 人在同一个房间。
人在同一个房间。
[思路分析] 由于每人可以进住任一房间,进住哪一个房间都有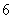 种等可能的方法,根据乘法原理,
种等可能的方法,根据乘法原理, 个人进住
个人进住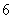 个房间有
个房间有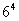 种方法,则(1)指定的
种方法,则(1)指定的 个房间中各有
个房间中各有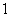 人有
人有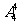 种方法,
种方法,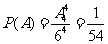 。
。
(2)恰有 个房间各有
个房间各有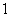 人有
人有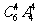 种方法,
种方法,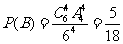 。(3)从
。(3)从 人中选
人中选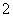 人的方法有
人的方法有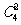 种,余下的
种,余下的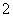 人每人都可以去另外的
人每人都可以去另外的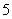 个房间中的任一间,有
个房间中的任一间,有 种方法,
种方法,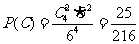 。(4)从
。(4)从 人中选
人中选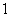 人去一号房间的方法有
人去一号房间的方法有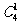 种,从余下
种,从余下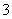 人中选
人中选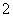 人去二号房间的方法有
人去二号房间的方法有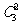 ,再余下的
,再余下的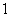 人可去
人可去 个房间中的任一间,
个房间中的任一间,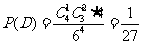 。
。
(5)从正面考虑情形较复杂,正难则反,“至少有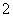 人在同一个房间”的反面是“没有
人在同一个房间”的反面是“没有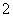 人在同一个房间,即恰有
人在同一个房间,即恰有 个房间各有
个房间各有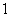 人”,
人”,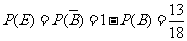 。
。
[简要评述] 本题考查等可能性事件的概率和互斥事件的概率,注意排列组合知识的运用。
例4、甲、乙、丙三人独立解某一道数学题,已知该题被甲解出而乙解不出的概率为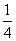 ,被乙解出而丙解不出的概率为
,被乙解出而丙解不出的概率为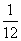 ,被甲、丙两人都解出的概率是
,被甲、丙两人都解出的概率是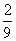 。
。
(1)求该题被乙独立解出的概率;
(2)求该题被解出的概率。
[思路分析](1)设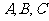 分别为甲、乙、丙三人各自独立解某一数学题的事件。由已知则有
分别为甲、乙、丙三人各自独立解某一数学题的事件。由已知则有
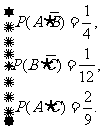 即
即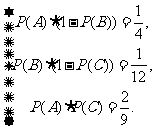 由此方程组解得
由此方程组解得 所以该题被乙独立解出的概率为
所以该题被乙独立解出的概率为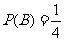 。
。
(2)记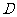 为该题被解出,它对应着甲、乙、丙三人中至少有一人解出该题,则
为该题被解出,它对应着甲、乙、丙三人中至少有一人解出该题,则
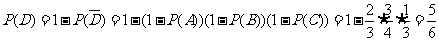 。
。
[简要评述] 本题考查相互独立事件的概率和互斥事件的概率,同时考查函数方程数学思想和运算能力。
[备选例题]
例5、某一汽车前进途中要经过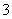 个红绿灯路口。已知汽车在第一个路口,遇到红灯和遇到绿灯的概率都是
个红绿灯路口。已知汽车在第一个路口,遇到红灯和遇到绿灯的概率都是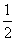 ;从第二个路口起,若前次遇到红灯,则下一次遇到红灯的概率是
;从第二个路口起,若前次遇到红灯,则下一次遇到红灯的概率是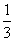 ,遇到绿灯的概率是
,遇到绿灯的概率是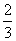 ;若前一次遇到绿灯,则下一次遇到红灯的概率是
;若前一次遇到绿灯,则下一次遇到红灯的概率是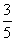 ,遇到绿灯的概率是
,遇到绿灯的概率是 。求:
。求:
(1)汽车在第二个路口遇到红灯的概率是多少?
(2)在三个路口中,汽车遇到一次红灯,两次绿灯的概率是多少? [思路分析] 根据相互独立事件同时发生的概率的乘法公式可得,
(1)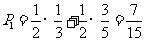 。
。
(2)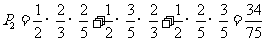 。
。
[简要评述] 本题重点考查相互独立事件的概率乘法公式的本质--同时发生,同时还考查互斥事件的概率。在具体解题中注意与递推有关的概率的计算。
[作业]
1.知识体系:
随机事件的概率:1等可能性事件的概率;2互斥事件的概率;3相互独立事件的概率;4独立重复实验。
3.突破此难点的关键在于:首先要运用两个基本原理认真审题,弄清楚问题属于四种类型事
件中的哪一种,然后准确地运用相应的公式进行计算,其中要注意排列、组合知识的应用。
[教学过程]
2.有关概率的实际应用问题。这种问题既考察逻辑思维能力,又考查运算能力;它要求对四
个概率公式的实质深刻理解并准确运用;要求计算概率,它一般以一小一大(既一道选择
题或填空题、一道解答题)的形式出现,属于中等偏难的题目。
[教学目标及重点、难点]
1.突出运算能力的考查。高考中的概率题目,均是用数值给出的选择支或要求用数值作答,
这就要求平时要重视用有关公式进行具体的计算。
16. 下列命题:
①动点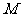 到二定点
到二定点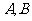 的距离之比为常数
的距离之比为常数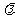 (
(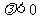 且
且 ),则动点
),则动点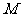 的轨迹是圆;
的轨迹是圆;
②椭圆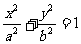 (
(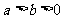 )的离心率为
)的离心率为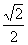 ,则
,则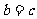 ;
;
③双曲线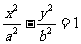 的焦点到渐近线的距离为
的焦点到渐近线的距离为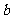 ;
;
④已知抛物线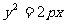 上两点
上两点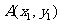 ,
,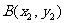 且
且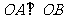 ,(
,(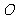 为坐标原点),则
为坐标原点),则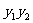 的值是
的值是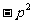 。
。
以上命题正确的是
15. 已知在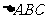 中,
中,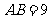 ,
,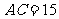 ,
,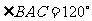 它所在平面外一点
它所在平面外一点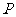 到
到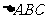 三个顶点的距离都是
三个顶点的距离都是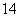 ,那么
,那么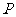 到平面
到平面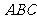 的距离是
的距离是
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com