
题目列表(包括答案和解析)
4.在∆ABC中,tanAtanB>1是∆ABC为锐角三角形的 ( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分又不必要条件
3.已知∆ABC中,a=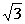 ,b=1,B=30o,则∆ABC的面积是 ( )
,b=1,B=30o,则∆ABC的面积是 ( )
A.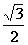 B.
B.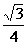 C.
C. 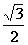 或
或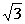 D.
D. 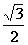 或
或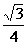
2.已知∆ABC中,角A,B,C的对边分别是a,b,c且A=60o,a=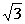 ,c=2,那么角C ( )
,c=2,那么角C ( )
A.有唯一的值 B.有两个不同的值 C.不存在 D.不能确定
1.在∆ABC中,A>B是sinA>sinB ( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分又不必要条件
10.设函数f(x)=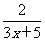 +
+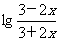 ,
,
(1)求函数f(x)的定义域;
(2)判断函数f(x)的单调性,并给出证明;
(3)已知函数f(x)的反函数f-1(x),问函数y=f-1(x)的图象与x轴有交点吗?若有,求出交点坐标;若无交点,说明理由.
解:(1)由3x+5≠0且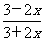 >0,解得x≠-
>0,解得x≠-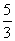 且-
且-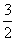 <x<
<x<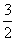 .取交集得-
.取交集得-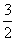 <x<
<x<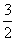 .
.
(2)令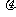 (x)=3x+5,随着x增大,函数值减小,所以在定义域内是减函数;
(x)=3x+5,随着x增大,函数值减小,所以在定义域内是减函数;
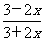 =-1+
=-1+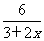 随着x增大,函数值减小,所以在定义域内是减函数.
随着x增大,函数值减小,所以在定义域内是减函数.
又y=lgx在定义域内是增函数,根据复合单调性可知,y=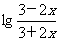 是减函数,所以f(x)=
是减函数,所以f(x)=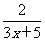 +
+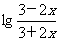 是减函数.
是减函数.
(3)因为直接求f(x)的反函数非常复杂且不易求出,于是利用函数与其反函数之间定义域与值域的关系求解.
设函数f(x)的反函数f-1(x)与工轴的交点为(x0,0).根据函数与反函数之间定义域与值域的关系可知,f(x)与y轴的交点是(0,x0),将(0,x0)代入f(x),解得x0=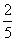 .所以函数y=f-1(x)的图象与x轴有交点,交点为(
.所以函数y=f-1(x)的图象与x轴有交点,交点为(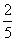 ,0)。
,0)。
欢迎访问
9.求函数y=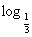 (x2-5x+4)的定义域、值域和单调区间.
(x2-5x+4)的定义域、值域和单调区间.
解:由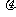 (x)=x2-5x+4>0,解得x>4或x<1,所以x∈(-∞,1)∪(4,+∞),当x∈(-∞,1)∪(4,+∞),{
(x)=x2-5x+4>0,解得x>4或x<1,所以x∈(-∞,1)∪(4,+∞),当x∈(-∞,1)∪(4,+∞),{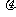 |
|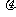 =x2-5x+4}=R+,所以函数的值域是R+.因为函数y=
=x2-5x+4}=R+,所以函数的值域是R+.因为函数y=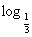 (x2-5x+4)是由y=
(x2-5x+4)是由y=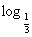
 (x)与
(x)与 (x)=x2-5x+4复合而成,函数y=
(x)=x2-5x+4复合而成,函数y=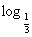
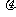 (x)在其定义域上是单调递减的,函数
(x)在其定义域上是单调递减的,函数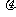 (x)=x2-5x+4在(-∞,
(x)=x2-5x+4在(-∞,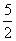 )上为减函数,在[
)上为减函数,在[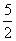 ,+∞]上为增函数.考虑到函数的定义域及复合函数单调性,y=
,+∞]上为增函数.考虑到函数的定义域及复合函数单调性,y=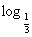 (x2-5x+4)的增区间是定义域内使y=
(x2-5x+4)的增区间是定义域内使y=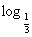
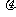 (x)为减函数、
(x)为减函数、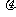 (x)=x2-5x+4也为减函数的区间,即(-∞,1);y=
(x)=x2-5x+4也为减函数的区间,即(-∞,1);y=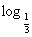 (x2-5x+4)的减区间是定义域内使y=
(x2-5x+4)的减区间是定义域内使y=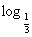
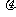 (x)为减函数、
(x)为减函数、 (x)=x2-5x+4为增函数的区间,即(4,+∞).
(x)=x2-5x+4为增函数的区间,即(4,+∞).
8.已知定义域为R的偶函数f(x)在[0,+∞]上是增函数,且f(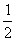 )=0,
)=0,
则不等式f(log4x)的解集是______.
解析:因为f(x)是偶函数,所以f(-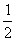 )=f(
)=f(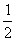 )=0.又f(x)在[0,+∞]上是增函数,所以f(x)在(-∞,0)上是减函数.所以f(log4x)>0
)=0.又f(x)在[0,+∞]上是增函数,所以f(x)在(-∞,0)上是减函数.所以f(log4x)>0 log4x>
log4x>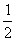 或log4x<-
或log4x<-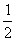 .
.
解得x>2或0<x<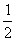 .
.
答案:x>2或0<x<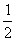
已知y=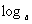 (2-ax)在[0,1]上是x的减函数,则a的取值范围是__________.
(2-ax)在[0,1]上是x的减函数,则a的取值范围是__________.
解析:a>0且a≠1
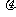 (x)=2-ax是减函数,要使y=
(x)=2-ax是减函数,要使y=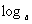 (2-ax)是减函数,则a>1,又2-ax>0
(2-ax)是减函数,则a>1,又2-ax>0 a<
a<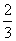 (0<x<1)
(0<x<1) a<2,所以a∈(1,2).
a<2,所以a∈(1,2).
答案:a∈(1,2)
7.函数f(x)的图象与g(x)=(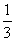 )x的图象关于直线y=x对称,则f(2x-x2)的单调递减区间为______.
)x的图象关于直线y=x对称,则f(2x-x2)的单调递减区间为______.
解析:因为f(x)与g(x)互为反函数,所以f(x)=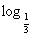 x
x
则f(2x-x2)=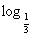 (2x-x2),令
(2x-x2),令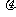 (x)=2x-x2>0,解得0<x<2.
(x)=2x-x2>0,解得0<x<2.
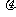 (x)=2x-x2在(0,1)上单调递增,则f[
(x)=2x-x2在(0,1)上单调递增,则f[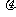 (x)]在(0,1)上单调递减;
(x)]在(0,1)上单调递减;
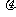 (x)=2x-x2在(1,2)上单调递减,则f[
(x)=2x-x2在(1,2)上单调递减,则f[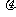 (x)]在[1,2)上单调递增.
(x)]在[1,2)上单调递增.
所以f(2x-x2)的单调递减区间为(0,1).
答案:(0,1)
5.函数y=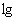 (
(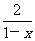 -1)的图象关于( )
-1)的图象关于( )
A.y轴对称 B.x轴对称
C.原点对称 D.直线y=x对称
解析:y=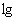 (
(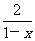 -1)=
-1)=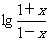 ,所以为奇函数.形如y=
,所以为奇函数.形如y=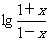 或y=
或y=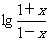 的函数都为奇函数.
的函数都为奇函数.
答案:C
4.若定义在区间(-1,0)内的函数f(x)=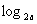 (x+1)满足f(x)>0,则a的取值范围为( )
(x+1)满足f(x)>0,则a的取值范围为( )
A.(0,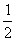 ) B.(0,
) B.(0,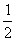 )
)
C.(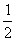 ,+∞) D.(0,+∞)
,+∞) D.(0,+∞)
解析:因为x∈(-1,0),所以x+1∈(0,1).当f(x)>0时,根据图象只有0<2a<l,解得0<a<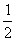 (根据本节思维过程中第四条提到的性质).
(根据本节思维过程中第四条提到的性质).
答案:A
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com