
题目列表(包括答案和解析)
13.某工厂8年来某产品产量y与时间t年的函数关系如下图,则:
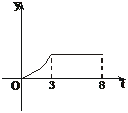
①前3年总产量增长速度增长速度越来越快;
②前3年中总产量增长速度越来越慢;
③第3年后,这种产品停止生产;
④第3年后,这种产品年产量保持不变.
以上说法中正确的是_______.
解析:由图分析,前3年总产量增长速度越来越快(曲线是下凸型),3年后,已不再生产.
答案:①③
12.函数f(x)=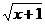 +
+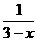 的定义域是_________.
的定义域是_________.
解析:要使函数有意义,只需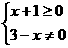
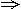
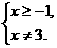
所以,这个函数的定义域是{x|x≥-1,x≠3}.
答案:{x|x≥-1,x≠3}
11.已知f(x)=x2-1(x<0),则f-1(3)=_______.
解析:设f-1(3)=x,则f(x)=3,即x2-1=3.
∴x=±2.∵x<0,∴x=-2.∴f-1(3)=-2.
答案:-2
10.已知f(x)=3ax+1-2a在(-1,1)上存在x0,使得f(x0)=0,则a的取值范围是
A.-1<a<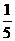 B.a>
B.a>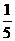
C.a>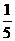 或a<-1 D.a<-1
或a<-1 D.a<-1
解法一:f(x0)=3ax0+1-2a=0,显然a≠0,
∴x0=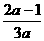 .由题意知-1<
.由题意知-1<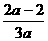 <1,解得a>
<1,解得a>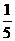 或a<-1.
或a<-1.
解法二:当a=0时,f(x)=1,不合题意.当a≠0时,问题转化为一次函数f(x)=3ax+1-2a的图象在(-1,1)上与x轴有交点,∴f(1)·f(-1)<0,即(a+1)(-5a+1)<0,解得a>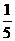 或a<-1.
或a<-1.
答案:C
第Ⅱ卷(非选择题 共70分)
9.若函数y=f(x)存在反函数y=f-1(x),则下列命题中不正确的是
A.若f(x)=f-1(x),则函数y=f(x)的图象关于y=x对称
B.函数y=f(x)的图象与直线y=x相交,则交点一定在它的反函数的图象上
C.若函数y=f(x)是(-∞,+∞)上的减函数,则其反函数y=f-1(x)也是(-∞,+∞)上的减函数
D.函数值域中的每一个值都有原象
解析:原函数y=f(x)是(-∞,+∞)上的减函数,则其反函数y=f-1(x)是原函数值域上的减函数.因为y=f(x)的值域未必是(-∞,+∞),故C不正确.
答案:C
8.某商场对顾客实行购物优惠活动,规定一次购物付款总额:
(1)如果不超过200元,则不给予优惠;
(2)如果超过200元但不超过500元,则按标价给予9折优惠;
(3)如果超过500元,其500元内的按第(2)条给予优惠,超过500元的部分给予7折 优惠.
某人两次去购物,分别付款168元和423元,假设他去一次购买上述同样的商品,则应付款是
A.413.7元 B.513.7元
C.546.6元 D.548.7元
解析:购物超过200元,至少付款200×0.9=180(元),超过500元,至少付款500×0.9=450(元),可知此人第一次购物不超过200元,第二次购物不超过500元,则此人两次购物总额是168+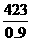 =168+470=638(元).
=168+470=638(元).
若一次购物,应付500×0.9+138×0.7=546.6(元).
答案:C
7.已知函数f(x)=ax2+bx+c的图象如下图所示,则b的取值范围是
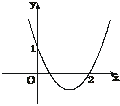
A.b>0 B.b<0
C.b<-1 D.-2<b<-1
解析:由图象得f(0)=1,即c=1.
由f(2)=0,得4a+2b+1=0.
对称轴-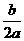 <2,a>0,
<2,a>0,
∴-b<4a=-2b-1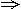 b<-1.
b<-1.
答案:C
6.已知集合A到集合B={0,1,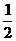 ,
,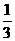 }的映射f:x→
}的映射f:x→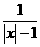 ,那么集合A中的元素最多有
,那么集合A中的元素最多有
A.3个 B.4个 C.5个 D.6个
解析:∵f是映射,∴A中的每一个元素都应在B中有象.
∵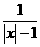 ≠0,∴0在A中不存在原象.
≠0,∴0在A中不存在原象.
当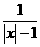 =1时,解得x=±2,
=1时,解得x=±2,
∴±2可作1的原象;
当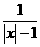 =
=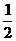 时,解得x=±3,
时,解得x=±3,
∴±3可作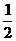 的原象;
的原象;
当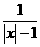 =
=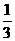 时,解得x=±4,
时,解得x=±4,
∴±4可作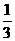 的原象.
的原象.
故A中的元素最多能有6个.
答案:D
5.对于任意x∈R,都有f(x+1)=2f(x),当0≤x≤1时,f(x)=x(1-x),则f(-1.5)的值是
A. B.
B.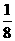
C.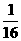 D.-
D.-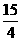
解析:令x=-1.5,由f(x+1)=2f(x)得f(-1.5)=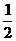 f(-0.5).
f(-0.5).
令x=-0.5,由f(x+1)=2f(x)得f(-0.5)=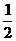 f(0.5).
f(0.5).
∴f(-1.5)=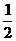 f(-0.5)=
f(-0.5)= f(0.5)=
f(0.5)= [0.5(1-0.5)]=
[0.5(1-0.5)]=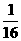 .
.
答案:C
4.函数f(x)=x2+2(a-1)x+2在区间(-∞,4]上递减,则a的取值范围是
A.[-3,+∞] B.(-∞,-3)
C.(-∞,5] D.[3,+∞)
解析:由-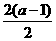 ≥-4,得a≤5.
≥-4,得a≤5.
答案:C
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com