
题目列表(包括答案和解析)
20、
(1)
由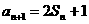 (n≥1)可得
(n≥1)可得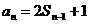 (n≥2),两式相减得
(n≥2),两式相减得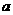 n+1-
n+1-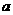 n=2
n=2 n,
n,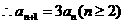 .
.
又 2=2S1+1=3,
2=2S1+1=3,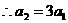 ,故{
,故{ n}是首项为1,公比为3的等比数列,
n}是首项为1,公比为3的等比数列,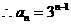 .
............6分
.
............6分
(2)设{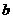 n}的公差为
n}的公差为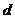 ,由T3=15可得
,由T3=15可得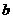 1+
1+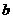 2+
2+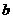 3=15,可得
3=15,可得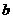 2=5,故可设
2=5,故可设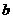 1=5-
1=5-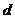 ,
,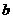 3=5+
3=5+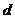 .
.
又 1=1,
1=1, 2=3,
2=3, 3=9,由题意可得(5-
3=9,由题意可得(5-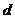 +1)(5+
+1)(5+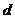 +9)=(5+3)2,解得
+9)=(5+3)2,解得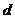 1=2,
1=2,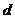 2=-10.
2=-10.
 等差数列{
等差数列{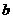 n}的各项为正,
n}的各项为正,
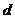 =2,
=2,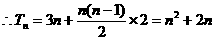 .
.
............12分
19、(1)由题设知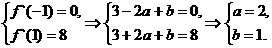
 ƒ(
ƒ(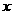 )=
)=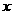 3+2
3+2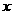 2+
2+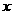 ,
............6分
,
............6分
(2)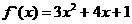 ,
,
令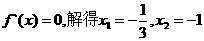 ,
............8分
,
............8分
当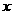 变化时,ƒ(
变化时,ƒ(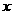 )
)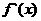 的变化情况如下表:
的变化情况如下表:
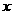 |
(- ,-1) ,-1) |
-1 |
(-1,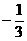 ) ) |
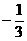 |
(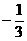 + + ) ) |
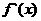 |
+ |
0 |
- |
0 |
+ |
ƒ(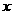 ) ) |
↑ |
0 |
↓ |
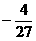 |
↑ |
 ƒ(
ƒ(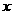 )的极大值为ƒ(-1)=0,极小值为ƒ(
)的极大值为ƒ(-1)=0,极小值为ƒ(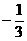 )=
)=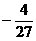 ........12分
........12分
18、解 设地面的长为x,则宽为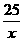 ,总造价为y,y=
,总造价为y,y=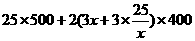 ............6分
............6分
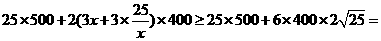 36500
36500
............10分
当且仅当x=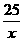 时取等,即长、宽相等都为5m时总造价最低为36500元
时取等,即长、宽相等都为5m时总造价最低为36500元
............12分
解:
二 13、21-2n 14、19 15、5 16、(1)(3)
17. 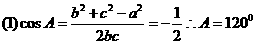 ............6分
............6分
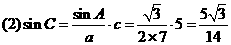 ............12分
............12分
22.(本小题满分14分)
已知函数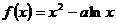 在
在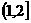 是增函数,
是增函数,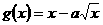 在(0,1)为减函数。
在(0,1)为减函数。
(1)求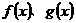 的表达式;
的表达式;
(2)当b>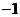 时,若对于任意的x∈(0,1 ],都有
时,若对于任意的x∈(0,1 ],都有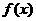 ≥
≥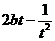 在
在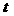 ∈(0,1 ]上恒成立,求b的取值范围.
∈(0,1 ]上恒成立,求b的取值范围.
2007-2008学年度上学期期末考试高二年级数学科试卷
文科答案
21.(本小题满分12分)已知曲线C上任意一点M到点F(0,1)的距离比它到直线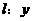 =
=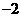 的距离小1.
的距离小1.
(1)求曲线C的方程;
(2)若过点P(2,2)的直线m与曲线C交于A,B两点,设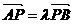 .
.
(i)当λ=1时,求直线m的方程;
(ii)当△AOB的面积为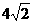 时(O为坐标原点),求λ的值.
时(O为坐标原点),求λ的值.
20.(本小题满分12分)数列{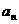 }的前n项和记为
}的前n项和记为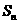 ,
,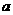 1=1,
1=1,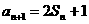 (n≥1).
(n≥1).
(1)
求{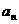 }的通项公式;
}的通项公式;
(2)
等差数列{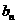 }的各项为正数,其前n项和为
}的各项为正数,其前n项和为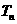 ,且
,且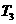 =15,又
=15,又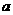 1+
1+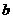 1,
1,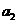 +
+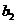 ,
,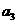 +
+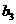 成等比数列,求
成等比数列,求 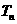
19.(本小题满分12分)定义在R上的函数ƒ(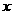 )=
)=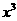 +
+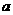
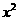 +
+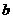
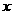 (
(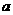 ,
,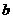 为常数),在
为常数),在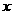 =-1处取得极值,ƒ(
=-1处取得极值,ƒ(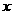 )的图象在P(1,
ƒ(1))处的切线平行直线
)的图象在P(1,
ƒ(1))处的切线平行直线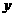 =8
=8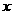 ,
,
(1)
求函数ƒ(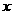 )解析式;
)解析式;
(2)
求函数ƒ(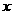 )极值。
)极值。
18.(本小题满分12分)要建一间地面面积为25m2,墙高为3m的长方体形的简易工棚,已知工棚屋顶每1m2的造价为500元,墙壁每1m2 的造价为400元。问怎样设计地面的长与宽,能使总造价最低?最低造价是多少?
17.(本小题满分12分)已知在△ABC中,角A、B、C所对的边分别为a,b,c, a=7, b=3, c=5,
(1)求△ABC中的最大角;
(2)求角C的正弦值。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com