
题目列表(包括答案和解析)
24、解:(1)若不采取任何预防措施,则总费用为400×0.3=120万元
(2)单独采用甲方案,则总费用为45+400×0.1=85万元
(3)单独采用乙方案,则总费用为30+400×0.15=90万元
(4)若甲、乙方案同时采用,则总费用为45+30+400×0.1×0.15=75.6万元
因此,当联合采用甲、乙两种方案时,总费用最少为75.6万元
C组答案
23、解:(1)设三人各射击一次,击中的人数为X,则X的分布列为
|
X |
0 |
1 |
2 |
3 |
|
P |
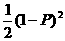 |
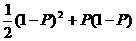 |
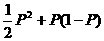 |
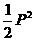 |
(2)由上表知
EX=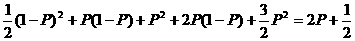
∴
2P+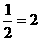 ∴ P=
∴ P=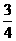
22、解:(1)由题知,总得分X的概率分布列为:
|
X |
-300 |
-100 |
100 |
300 |
|
P |
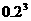 |
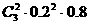 |
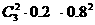 |
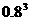 |
∴ EX=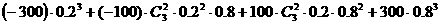
=180
P(X≥100)= P(X=100)+P(X=300)
=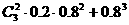
=0.896
12、解:⑴由条件得: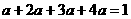
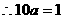 得
得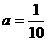
⑵由已知可列出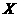 的分布列如下:
的分布列如下:
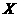 |
1 |
2 |
3 |
4 |
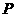 |
0.1 |
0.2 |
0.3 |
0.4 |
⑶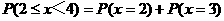
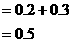
B组答案
13-17. BABDD 18. 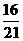 19. 15 20.
19. 15 20.
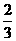 21. 0.135
21. 0.135
11、解:随机变量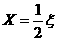 的分布列为:
的分布列为:
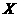 |
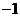 |
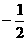 |
0 |
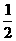 |
1 |
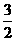 |
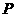 |
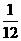 |
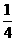 |
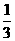 |
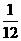 |
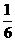 |
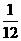 |
随机变量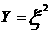 的分布列为:
的分布列为:
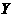 |
0 |
1 |
4 |
9 |
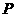 |
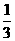 |
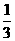 |
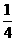 |
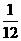 |
10、解:记“第一次抽到次品”的事件为A, “第二次抽到次品”的事件为B,则“第一次和第二次都抽到次品”的事件为AB,
⑴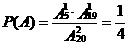 ⑵
⑵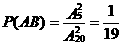
⑶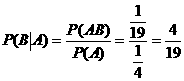
28、设b和c分别是先后抛掷一枚骰子得到的点数,用随机变量X表示方程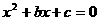 实根的个数(重根按一个计).
实根的个数(重根按一个计).
(1)求方程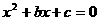 有实根的概率;
有实根的概率;
(2)求X的分布列和数学期望;
(3)求在先后两次的点数中有5的条件下,方程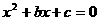 有实根的概率.
有实根的概率.
A组答案
1-5. BDCCC 6. 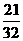 7.
7.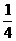 ,
, 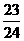 8.
8.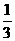 9.
9.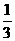
27、某陶瓷厂准备烧制三件不同的工艺品,制作过程必须先后经过两次烧制,当第一次烧制合格后方可进入第二次烧制,两次烧制过程相互独立.根据该厂现有的技术水平,经过第一次烧制后,甲、乙、丙三件产品合格的概率依次为0.5, 0.6, 0.4 . 经过第二次烧制后,甲、乙、丙三件产品合格的概率依次为0.6, 0.5, 0.75.
(1)求第一次烧制后恰有一件产品合格的概率;
(2)经过前后两次烧制后,合格工艺品的个数为ξ,求随机变量ξ的期望.
26、已知P随机变量X-N(μ,σ2),且其正态曲线在(-∞,80)上是增函数,在
(80,+∞)上为减函数,且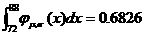 ,则
,则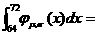 ________.
________.
25、口袋里放有大小相等的两个红球和一个白球,有放回地每次摸取一个球,定义数列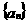 ,
, ,如果
,如果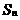 为数列
为数列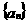 的前
的前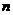 项和,那么
项和,那么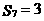 的概率为( )
的概率为( )
A、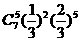 B、
B、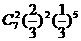 C、
C、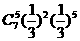 D、
D、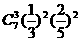
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com