
(1)设I为全集,M、N、P都是它的子集,则图中阴影部分表示的集合是
(A)M∩[(C1N)∩P] (B)M∩n(N ∪ P)
(C)[(C1M)∩(C1N)]∩P (D)M∩N ∪(N∩P)
(2)如图,圆锥的底面半径为1,高为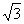 ,则圆锥的表面积为
,则圆锥的表面积为
(A) 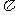 (B)2
(B)2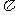
(C)3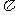 (D)4
(D)4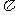
(3)从一箱苹果中任取一个,如果其重量小于200克的概率为0.2,重量在[200,300]克的概率为0.5,那么重量超过300克的概率为
(A)0.2 (B)0.3 (c)0.7 (D)0.8
(4)下列函数中,周期为1的奇函数为
(A)y=sinxcosx (B)y=1-2sin2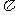 x
x
(c)y=cos2(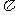 x一
x一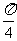 )一
)一 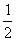 (D)y=tan
(D)y=tan 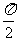 x
x
(5)等比数列{a n}的公比q=2,a1 + a 2 + a 3 = 21,贝a 3 + a 4 + a 5= ( )
(A)42 (B)63 (c)84 (D)168
(6)过点M(1,2)的直线l与圆C:(x一2)2+y 2=9交于A、B两点:C为圆心,当∠ACB最小时,直线l的方程为
(A)x = l (B)y = l (C)x-y + l= 0 (D)x一2y+3=0
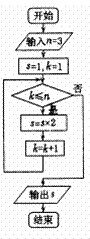 (7)右图所示的程序框图的输出结果为
(7)右图所示的程序框图的输出结果为
(A)2 (B)4
(c)8 (D)16
(8)在四边形ABCD中,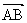 = a+2b,
= a+2b,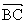 = 一4a-b,
= 一4a-b,
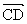 = 一5 a一3 b,
= 一5 a一3 b,
则四边形ABCD的形状是
(A)长方形 (B)平行四边形
(C)梯形 (D)以上都不对
(9)抛物线Y=4x2上的一点M到焦点的距离为1,则点M的纵坐标是
(A)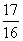 17
(B)
17
(B)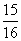
(C) 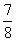 (D)1
(D)1
(10)从100张卡片(卡号为l号到100号)中任取一张,取到卡号为7的倍数的概翠是
(A)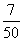 (B)
(B)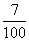 7 (C)
7 (C)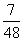 (D)
(D)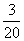
(11)从甲、乙两人手工制作的圆形产品中,各自随机抽取6件,测得其直径如下(单位:cm):
甲:9.00, 9.20, 9.00,8.50, 9.10, 9.20
乙:8.90, 9.60, 9.50,8.50,8.60,8.90
据以上数据估计两人的技术稳定性,结论是
(A)甲优于乙 (B)乙优于甲 (C)两人没区别 (D)无法判断
(12)以下三个命题:
① 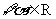 ,在[
,在[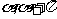 ]上函数Y=sinx都能取到最大值1;
]上函数Y=sinx都能取到最大值1;
②若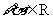 且a≠0,f(x+a)= 一
f(x)对
且a≠0,f(x+a)= 一
f(x)对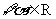 成立,则f(x)为周期函数;
成立,则f(x)为周期函数;
③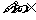 (一
(一 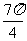 ,一
,一 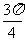 ),使sinx<cosx.
),使sinx<cosx.
其中正确命题的个数为
(A)0 (B)l (C)2 (D)3
第Ⅱ卷(非选择题共90分)
22.(13分)
设函数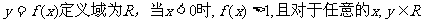 ,有
,有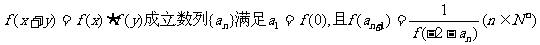 。
。
(1)求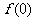 的值;
的值;
(2)求数列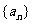 的通项公式;
的通项公式;
(3)是否存在正数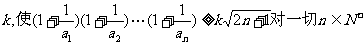 均成立,若存在,求出k的最大值,并证明,否则说明理由。
均成立,若存在,求出k的最大值,并证明,否则说明理由。
21.(13分)
已知△OFQ的面积为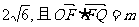 ,
,
(1)设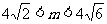 ,求向量
,求向量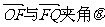 的取值范围;
的取值范围;
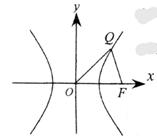 (2)设以O为中心,F为焦点的双曲线经过点Q(如图),若
(2)设以O为中心,F为焦点的双曲线经过点Q(如图),若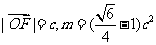 ,
,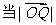 取最小值时,求此双曲线的方程。
取最小值时,求此双曲线的方程。
20.(13分)
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD是直角梯形,∠BAD=90º,AD∥BC,AB=BC=1,AD=3,PD与底面ABCD成30º角。
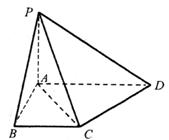 (1)求点A到平面PBC的距离;
(1)求点A到平面PBC的距离;
(2)求二面角A-PC-B的平面角大小;
19.(13分)
海岛上有一座海拔1000米的山,山顶上设有一个灯塔A,上午11时,灯塔A处的值班员测得一匀速行驶的轮船在岛北偏东60º的C处,由A观察C的俯解为30º,11时10分又测得该船在岛北偏西60º的B处,由A观察B的俯角为60º。
(1)求该船的速度(单位:千米/小时);
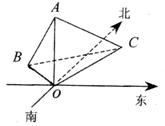 (2)轮船在沿航线CB航行中,船上的瞭望员随时观测灯塔发出的导航信号,试问瞭望员在整个观测过程中,观测仰角最大是多少?
(2)轮船在沿航线CB航行中,船上的瞭望员随时观测灯塔发出的导航信号,试问瞭望员在整个观测过程中,观测仰角最大是多少?
18.(12分)
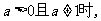 解关于x的不等式
解关于x的不等式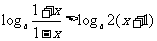
17.(12分)
如图,正三棱柱ABC-A1B1C1中点E、F分别是AB1和AB的中点,
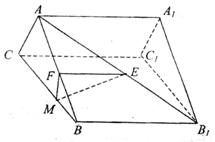 (1)求证:BB1∥平面EFM;
(1)求证:BB1∥平面EFM;
(2)若FM⊥BC于点M,求证:ME⊥BC。
16.ABCD-A1B1C1D1是单位正方体,黑、白两只蚂蚁从点A出发沿棱向前爬行,每爬完一条棱称为“爬完一段”。白蚂蚁爬行的路线是AA1→A1D→…,黑蚂蚁爬行的路线是AB→
BB1→…,它们都遵循如下规律:所爬行的第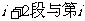 段所在直线必须是异面直线(其中
段所在直线必须是异面直线(其中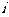 是自然数)。设黑、白蚂蚁都爬完2006段后各自停止在正方体的某个顶点处,此时黑、白蚂蚁的距离是
是自然数)。设黑、白蚂蚁都爬完2006段后各自停止在正方体的某个顶点处,此时黑、白蚂蚁的距离是
15.若二面角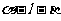 的平面角大小为
的平面角大小为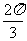 ,直线
,直线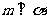 ,则平面
,则平面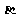 内的直线与m所成角的取值范围是
内的直线与m所成角的取值范围是
14.若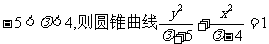 的焦点坐标为
的焦点坐标为
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com