
5.直线a∥平面  ,
, 内有n条直线交于一点,则这n条直线中与直线a平行的直线
内有n条直线交于一点,则这n条直线中与直线a平行的直线
A.至少有一条 B.至多有一条 C.有且只有一条 D. 没有
4.在区间[3,5]上有零点的函数是
A.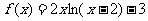 B.
B.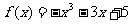
C.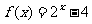 D.
D.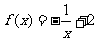
3.用若干个大小相同,棱长为1的正方体摆成一个立体模型,其三视图如下
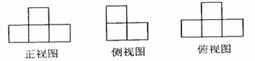
根据三视图回答此立体模型的体积为
A.4 B.5 C. 6 D.7
2.给出关于满足A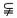 B的非空集合A、B的四个命题
B的非空集合A、B的四个命题
①若任取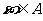 ,则
,则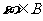 是必然事件
是必然事件
②若任取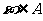 ,则
,则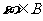 是不可能事件
是不可能事件
③若任取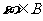 ,则
,则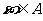 是随机事件
是随机事件
④若任取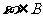 ,则
,则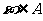 是必然事件
是必然事件
其中正确的命题有
A. 1个 B.2个 C.3个 D.4个
1.复数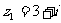 ,
,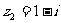 ,则
,则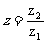 在复平面内对应的点位于
在复平面内对应的点位于
A.第一象限 B.第二象限 C. 第三象限 D. 第四象限
22.(本小题满分14分)
已知等比数列{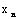 }的各项为不等于1的正数,数列{
}的各项为不等于1的正数,数列{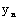 }满足
}满足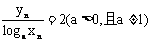 ,设y3=18,y6=12
,设y3=18,y6=12
(1)数列{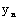 }的前多少项和最大,最大值为多少?
}的前多少项和最大,最大值为多少?
(2)试判断是否存在自然数M,使得当n>M时,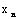 >1恒成立,若存在,求出最小的自然数M;若不存在,请说明理由;
>1恒成立,若存在,求出最小的自然数M;若不存在,请说明理由;
(3)令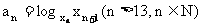 ,试比较
,试比较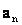 与
与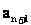 的大小。
的大小。
21. (本小题满分12分)
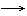
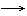 已知点F(0,a)(a>0)。点P在x轴上运动,点M在y轴上运动,满足① PM· PF=0;
已知点F(0,a)(a>0)。点P在x轴上运动,点M在y轴上运动,满足① PM· PF=0;
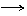
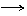
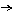 ②PN+
②PN+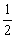 NM= 0
NM= 0
(I)求点N的轨迹E的方程
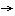
 (Ⅱ)过点F的直线l与曲线E交于A、B两点,设K(0,-a),KA与KB的夹角为
(Ⅱ)过点F的直线l与曲线E交于A、B两点,设K(0,-a),KA与KB的夹角为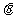 ,求证:
,求证: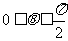 。
。
20.(本小题满分12分)
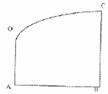 某地政府为科技兴市,欲将如图所示的一块不规则的非农业用地规划建成一个矩形高科技工业园区。已知AB⊥BC,OA∥BC,且AB=BC=2AO=4千米,曲线段OC是以点0为顶点且开口向右的抛物线的一段.如果要使矩形园区的相邻两边分别落在AB、BC上,且一个顶点落在曲线段OC上,问应如何规划才能使矩形工业园区的用地面积最大?并求出最大的用地面积(精确到0.1km2)。
某地政府为科技兴市,欲将如图所示的一块不规则的非农业用地规划建成一个矩形高科技工业园区。已知AB⊥BC,OA∥BC,且AB=BC=2AO=4千米,曲线段OC是以点0为顶点且开口向右的抛物线的一段.如果要使矩形园区的相邻两边分别落在AB、BC上,且一个顶点落在曲线段OC上,问应如何规划才能使矩形工业园区的用地面积最大?并求出最大的用地面积(精确到0.1km2)。
19.(本小题满分12分)
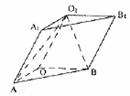 如图,在三棱柱OAB-O1A1B1中,平面OBB1O1⊥平面OAB,∠O1OB=60°,∠AOB=90°,且OB=OO1=2,OA=
如图,在三棱柱OAB-O1A1B1中,平面OBB1O1⊥平面OAB,∠O1OB=60°,∠AOB=90°,且OB=OO1=2,OA=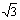 。
。
(1)求证:平面AOO1A1⊥平面OBB1O1;
(2)求二面角O1-AB-O的平面角的正切值。
(3)求异面直线A1B与AO1所成角的余弦值。
18.(本小题满分12分)
某高校最近出台一项计算机学分认定考试规定:每位同学一年之内最多有4次参加计算机考试的机会,一旦某次考试通过,便可获得计算机科目的学分,不再参加以后的考试,否则就一直考到第4次为止。如果李祥决定参加计算机科目考试,设他每次参价考试通过的概率依次为0.6,0.7,0.8,0.9,求在一年内李祥参加计算机科目考试次数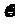 的分布列和
的分布列和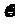 的期望,并求李祥在一年内获得计算机科目学分的概率。
的期望,并求李祥在一年内获得计算机科目学分的概率。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com