
22.(本小题满分14分)
已知直线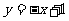 与椭圆
与椭圆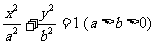 相交于A、B两点.
相交于A、B两点.
(Ⅰ)若椭圆的离心率为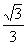 ,焦距为2,求线段AB的长;
,焦距为2,求线段AB的长;
(Ⅱ)若向量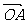 与向量
与向量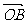 互相垂直(其中O为坐标原点),当椭圆的离心率
互相垂直(其中O为坐标原点),当椭圆的离心率
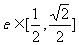 时,求椭圆的长轴长的最大值.
时,求椭圆的长轴长的最大值.
21.(本小题满分12分)
已知正项数列 的前n项和为
的前n项和为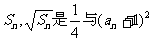 的等比中项.
的等比中项.
(Ⅰ)求证:数列 是等差数列;
是等差数列;
(Ⅱ)若 ,数列
,数列 的前n项和为Tn,求Tn;
的前n项和为Tn,求Tn;
(Ⅲ)在(Ⅱ)的条件下,是否存在常数λ,使得数列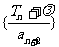 为等比数列?若存在,试求出λ;若不存在,说明理由.
为等比数列?若存在,试求出λ;若不存在,说明理由.
20.(本小题满分12分)
已知函数
(Ⅰ)当a = 1时,求函数f (x)在点x = 1处的切线方程;
(Ⅱ)求函数f (x)的极值;
(Ⅲ)若函数f (x)在区间(2,+∞)上是增函数,试确定a的取值范围.
19.(本小题满分12分)
设函数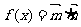 ,其中向量
,其中向量 .
.
(Ⅰ)求f (x)的最小正周期与单调递减区间;
(Ⅱ)在△ABC中,a、b、c分别是角A、B、C的对边,已知f (A) =2,b = 1,△ABC的面积为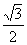 ,求
,求 的值.
的值.
18.(本小题满分12分)
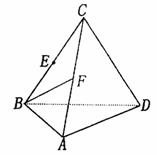
如图,四面体C-ABD,CB = CD,AB = AD, ∠BAD = 90°.E、F分别是BC、AC的中点.
(Ⅰ)求证:AC⊥BD;
(Ⅱ)如何在AC上找一点M,使BF∥平面MED?并说明理由;
(Ⅲ)若CA = CB,求证:点C在底面ABD上的射影是线段BD的中点.
17.(本小题满分12分)
某种商品两次提价,有两种提价方案,方案甲是第一次提价p%,第二次提价q%(其中p>q>0);方案乙是第一次提价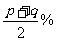 ,第二次提价
,第二次提价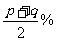 ,试比较两种提价方案中哪种提价多?并说明理由.
,试比较两种提价方案中哪种提价多?并说明理由.
16.下列结论:
①已知命题p: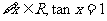 ;命题q:
;命题q:
则命题“ ”是假命题;
”是假命题;
②函数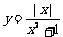 的最小值为
的最小值为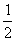 且它的图像关于y轴对称;
且它的图像关于y轴对称;
|
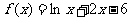 在定义域上有且只有一个零点;
在定义域上有且只有一个零点;
④“a = 1”是“圆x2 + y2-2x-2y = 0上有3个点到直线x + y-a = 0的距离都等于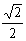 ”的充要条件.
”的充要条件.
其中正确命题的序号为 .(把你认为正确的命题序号都填上)
15.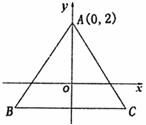 如图,在直角坐标系xoy中,O是正△ABC的中心, A点
如图,在直角坐标系xoy中,O是正△ABC的中心, A点
的坐标为(0,2),动点P(x,y)是△ABC内的点(包括
边界).若目标函数z = ax + by的最大值为2,且此时的最
优解(x,y)确定的点P(x,y)是线段AC上的所有点,则目
标函数z = ax + by的最小值为 .
14.设函数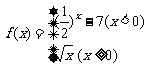 ,若f(a)
< 1,则实数a的取值范围是
.
,若f(a)
< 1,则实数a的取值范围是
.
13.防疫站对学生进行身体健康调查,采用分层抽样法抽取.红星中学共有学生1600名,抽取一个容量为200的样本.已知女生比男生少抽了10人,则该校的女生人数应是 人.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com