当b=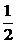时，G、F、H三点的横坐标均为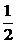，故三点共线；

71.（Ⅰ）解：由△OBC三顶点坐标O（0，0），B（1，0），C（b，c）（c≠0），可求得重心G（），外心F（），垂心H（b，）.

即m的取值范围为（－，0）∪（0，）.

解得0＜|m|＜.

x²=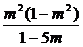

∵1－m²＞0

∴1－5m²＞0

              ②

将①式代入②，并解得

70.解：设点P的坐标为（x，y），依题设得=2，即

y=±2x，x≠0               ①

因此，点P（x，y）、M（－1，0）、N（1，0）三点不共线，得

||PM|－|PN||＜|MN|=2

∵||PM|－|PN||=2|m|＞0

∴0＜|m|＜1

因此，点P在以M、N为焦点，实轴长为2|m|的双曲线上，故

注：在推导过程中，未写明“x₁≠x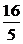₂”“k≠0”“k=0时也成立”及把结论写为“－≤m≤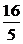”的均不扣分.

所以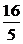－＜m＜.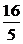

由P（4，y₀）在线段BB′（B′与B关于x轴对称，如图8―18）的内部，得－＜y₀＜.