
则|x0|= =4,代入
=4,代入 =1,得y02=
=1,得y02=
 54.答案:
54.答案:
解析:如图8―15所示,设圆心P(x0,y0)
53.答案:(2,2)
解析:将曲线方程化为(y-2)2=-4(x-2).
令x′=x-2,y′=y-2,则y′2=-4x′,∴h=2,k=2
∴坐标原点应移到(2,2).
∴ ,即e=
,即e=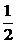
评述:本题重点考查了椭圆的基本性质.
∴ ∴
∴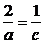
解析:由题意知过F1且垂直于x轴的弦长为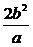
52.答案: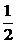
解得 和
和 ,
,
所以焦点坐标为(6,0),(-4,0).
又由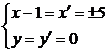
把上式化为标准方程为 =1.
=1.
在新坐标系下易知焦点坐标为(±5,0),
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com