
 ①
①
由点C、E在双曲线上,将点C、E的坐标和e= 代入双曲线方程得
代入双曲线方程得
设双曲线的方程为 ,则离心率e=
,则离心率e= .
.
由定比分点坐标公式得 .
.
依题意,记A(-c,0),C( ,h),E(x0,y0),其中c=
,h),E(x0,y0),其中c=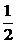 |AB|为双曲线的半焦距,h是梯形的高.
|AB|为双曲线的半焦距,h是梯形的高.
81.解:以AB的垂直平分线为y轴,直线AB为x轴,建立直角坐标系xOy,则CD⊥y轴,因为双曲线经过点C、D,且以A、B为焦点,由双曲线的对称性知C、D关于y轴对称.
因为A、B是原点以外的两点,所以x≠0.
所以点M的轨迹是以(2p,0)为圆心,以2p为半径的圆,去掉坐标原点.
评述:本小题主要考查直线、抛物线的基础知识,考查由动点求轨迹方程的基本方法以及方程化简的基本技能.
∴x2+y2-4px=0.
由③、④两式得- +yByA-(x2+y2)=0,
+yByA-(x2+y2)=0,
由①式知,yAyB=-16p2,
整理得, yA2+yyA-(x2+y2)=0 ④
yA2+yyA-(x2+y2)=0 ④
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com