
∴a=5,∴b= =4
=4
37.答案: =1
=1
解析:由两焦点坐标得出椭圆中心为点(2,0),焦半径c=3
∵长轴长为10,∴
 =4.∴y1+y2=4,即y0=2,x0=y0+1=3.
=4.∴y1+y2=4,即y0=2,x0=y0+1=3.
故中点为P(3,2).
评述:本题考查曲线的交点与方程的根的关系.同时应注意解法一中的纵坐标与解法二中的横坐标的求法.
∴x0= =3.y0=x0-1=2.∴P(3,2).
=3.y0=x0-1=2.∴P(3,2).
解法二:y22=4x2,y12=4x1,y22-y12=4x2-4x1
由题意得 ,(x-1)2=4x,x2-6x+1=0.
,(x-1)2=4x,x2-6x+1=0.
36.答案:(3,2)
解法一:设直线y=x-1与抛物线y2=4x交于A(x1,y1),B(x2,y2),其中点为P(x0,y0).
解得b2=2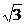 .
.
评述:本题主要考查椭圆的基本知识以及基本计算技能,体现出方程的思想方法.
∴点P的横、纵坐标分别为 c,即P(1,
c,即P(1,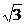 )在椭圆上,所以有
)在椭圆上,所以有 =1,又b2+c2=a2,
=1,又b2+c2=a2,
解析:因为F1、F2为椭圆的焦点,点P在椭圆上,且正△POF2的面积为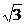 ,所以S=
,所以S=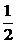 |OF2|?|PO|sin60°=
|OF2|?|PO|sin60°= c2,所以c2=4.
c2,所以c2=4.
35.答案:2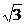
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com