
当a2+ <1时,Δ<0,曲线l与椭圆C没有交点.
<1时,Δ<0,曲线l与椭圆C没有交点.
因为(0,0)在椭圆C内,又在曲线l上,所以曲线l在椭圆C内.
故点Q的轨迹方程为2x2+y2-2ax-by=0;
所以当a2+ =1时,Δ=0,曲线l与椭圆C有且只有一个交点P(a,b);
=1时,Δ=0,曲线l与椭圆C有且只有一个交点P(a,b);
因为Δ=8b2(a2+ -1),由已知a2+
-1),由已知a2+ ≤1
≤1
则由 得(
得(
综上所述,点Q的坐标满足方程2x2+y2-2ax-by=0.
设方程⑦所表示的曲线为l.
由⑤、⑥及 ,
,
得点Q的坐标满足方程2x2+y2-2ax-by=0 ⑦
当x1=x2时,k不存在,此时l平行于y轴,因此AB的中点Q一定落在x轴,即Q的坐标为(a,0),显然点Q的坐标满足方程⑦
①-②得(x1+x2)(x1-x2)+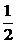 (y1+y2)(y1-y2)=0. ⑤
(y1+y2)(y1-y2)=0. ⑤
③+④得y1+y2=k(x1+x2)-2ka+2b ⑥
由已知x12+ =1 ①,x22+
=1 ①,x22+ =1 ②
=1 ②
y1=k(x1-a)+b ③,y2=k(x2-a)+b ④
77.解:(1)设点A、B的坐标分别为(x1,y1)、(x2,y2),点Q的坐标为Q(x,y).
当x1≠x2时,设直线斜率为k,则l的方程为y=k(x-a)+b.
∴|EN|= =|NF|.
=|NF|.
评述:该题的解答既可采用常规的坐标法,借助代数推理进行,又可采用圆锥曲线的几何性质,借助平面几何的方法进行推理.解题思路宽,而且几何方法较之解析法比较快捷便当.从审题与思维深度上看,几何法的采用,源于思维的深刻.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com