则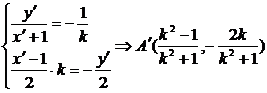
95.解：如图8―26所示，由题意设抛物线C的方程为y2＝2px（p>0），且x轴和y轴不是所求直线，又L过原点，因而可设L的方程为y=kx（k≠0），设A′B′分别是A、B关于L的对称点．
A′（x′，y′）关于y=kx对称于A（－1，0）
所以，点Q的轨迹以（1，0）为中心，长、短半轴长分别为1和
且长轴在x轴上的椭圆，去掉坐标原点.
评述：本题主要考查直线、椭圆的方程和性质，曲线与方程的关系，轨迹的概念和求法等解析几何的基本思想及综合运用知识的能力.
（x－1）2+
=1（x＞0）.
.
将①、②、③代入上式，整理得点Q的轨迹方程
由点O、Q、R共线，得
,即
③
由题设|OQ|?|OP|=|OR|2，得
|
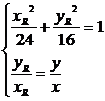
94.如图8―25，设点P、Q、R的坐标分别为（12，yP），（x，y），（xR，yR），由题设知xR＞0，x＞0.
的取值范围为（2－
，1）∪（1，＋∞）．
.