
(1)当m>n,即 <1时,因为
<1时,因为 +m2tanθ≥2nm,当且仅当tan2θ=
+m2tanθ≥2nm,当且仅当tan2θ= 时等号成立,所以
时等号成立,所以 .
.
(Ⅱ)S= .
.
93.(Ⅰ)设经过原点且倾角为θ的直线方程为y=xtanθ,可得方程组 又由对称性,得四边形ABCD为矩形,同时0<θ<
又由对称性,得四边形ABCD为矩形,同时0<θ<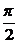 ,所以四边形ABCD的面积S=4|xy|=
,所以四边形ABCD的面积S=4|xy|= .
.
所以点Q的轨迹是以(1,1)为中心,长、短半轴分别为 和
和 ,且长轴与x轴平行的椭圆,去掉坐标原点.
,且长轴与x轴平行的椭圆,去掉坐标原点.
评述:本题主要考查直线、椭圆的方程和性质,曲线与方程的关系,轨迹的概念和求法,利用方程判定曲线的性质等解析几何的基本思想和综合运用知识的能力.
将①②③④代入⑤⑥,整理得点Q的轨迹方程为 =1(其中x、y不同时为零)
=1(其中x、y不同时为零)
92.解:由题设知点Q不在原点,设P、R、Q的坐标分别为(xP,yP),(xR,yR),(x,y),其中x、y不同时为零.
设OP与x轴正方向的夹角为α,则有
xP=|OP|cosα,yP=|OP|sinα
xR=|OR|cosα,yR=|OR|sinα
x=|OQ|cosα,y=|OQ|sinα
由上式及题设|OQ|?|OP|=|OR|2,得
|