|
试题详情
四、回顾总结: 本课主要研究垂直直接证明方法 1、已知长方体ABCD-A1B1C1D1中,底面ABCD是正方形且AB=1,AA1=2,点E为CC1的中点,点F为BD1中点,求证EF为BD1和CC1的公垂线 试题详情
2、如图,直三棱柱ABC-A1B1C1中,∠ACB=900,AC=1,CB= ,侧棱AA1=1,侧面AA1B1B的两条对角线的交点为D,B1C1的中点为M,求证:CD⊥平面BDM ,侧棱AA1=1,侧面AA1B1B的两条对角线的交点为D,B1C1的中点为M,求证:CD⊥平面BDM 试题详情
试题详情
3、在棱长为1的正方体ABCD-A1B1C1D1中,点E是棱BC的中点,点F是棱CD上的点,试确定点F的位置,使得D1E⊥平面AB1F 试题详情
4、四棱锥P-ABCD中,底面ABCD是矩形,AB=1,BC=a(a>1),PA⊥平面ABCD,PA=1,点Q在BC上,问是否对任意的a>1,都存在Q∈BC使得PQ⊥DQ?证明你的结论。 试题详情
试题详情
4、a≥2时,存在点Q(1, ,0);当1<a<2时,不存在满足条件的点Q ,0);当1<a<2时,不存在满足条件的点Q 试题详情
3.2.2空间线面关系的判定(2)-----空间线面、面面关系 [教学目标] [教学重点]用向量方法判断空间线面平行与垂直关系 [教学难点]用向量方法判断空间线面平行与垂直关系 [教学过程] 一、复习引入 试题详情
三、情感态度与价值观:体会向量的方法 1、用向量研究空间线面关系,设空间两条直线 的方向向量分别为 的方向向量分别为 ,两个平面 ,两个平面 的法向量分别为 的法向量分别为 ,则由如下结论 ,则由如下结论 平 行 垂 直 试题详情
 与 与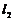
试题详情
试题详情
试题详情
 与 与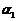
试题详情
试题详情
试题详情
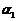 与 与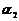
试题详情
试题详情
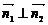
二、数学运用 试题详情
试题详情
证明:以 、 、 、 、 为正交基底,建立如图所示空间坐标系,设AN=xAE,AB,AD,AF长分别为3a,3b,3c,B(3a,0,0),D(0,3b,0),F(0,0,3c),E(0,3b,3c) 为正交基底,建立如图所示空间坐标系,设AN=xAE,AB,AD,AF长分别为3a,3b,3c,B(3a,0,0),D(0,3b,0),F(0,0,3c),E(0,3b,3c) 试题详情
 =(-3a,3b,0), =(-3a,3b,0), =(0,-3b,-3c) =(0,-3b,-3c)
试题详情
试题详情
(2a,(-3x+1)b,xc)又平面CDE的一个法向量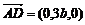 试题详情
NM//平面ECD,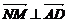 试题详情
试题详情
试题详情
 例2、在正方体 例2、在正方体 中,E,F分别是BB1,,CD中点,问过D1F的任何一个平面是否垂直平面ADE? 中,E,F分别是BB1,,CD中点,问过D1F的任何一个平面是否垂直平面ADE?
分析:只要验证D1F是否垂直平面ADE即可 证明:设正方体棱长为1,建立如图所示坐标系D-xyz 试题详情
 , ,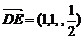
试题详情
因为 所以 所以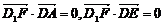 试题详情
试题详情
试题详情
试题详情
例3、四棱锥P-ABCD底面是一直角梯形,AB∥CD,AB⊥AD,CD=2AB,PA⊥平面ABCD,E为PC的中点(1)求证:BE∥平面PAD;(2)平面EBD是否垂直平面ABCD,证明你的结论 试题详情
[方法一]原来思路⑴取PD的中点F,FE AB,ABEF是平行四边形,BE∥AF,BE、AF分别在平面PAD外、内,故:BE∥平面PAD AB,ABEF是平行四边形,BE∥AF,BE、AF分别在平面PAD外、内,故:BE∥平面PAD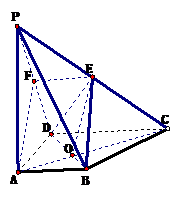 ⑵如果平面EBD⊥平面ABCD,交线为BD,则过E作EO⊥BD,EO⊥平面ABCD,∵PA⊥平面ABCD∴EO∥PA ∵E为PC中点∴O为AC的中点
∵ABCD是直角梯形∴O不在BD上,与O在BD上矛盾,平面EBD不垂直平面ABCD 试题详情
试题详情
试题详情
试题详情
设D(-a,0,0),B(0,b,0),
P(0,0,c),则C(-a,2b,0),E(- ,b, ,b, ), ), 试题详情
试题详情
试题详情
⑵平面ABCD的法向量为 =P(0,0,c),设平面BED的法向量为 =P(0,0,c),设平面BED的法向量为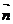 =(x,y,z),则 =(x,y,z),则 试题详情
试题详情
试题详情
四.布置作业: 1、如图E、F、G、H分别为正方体AC1的棱A1B1、A1D1、B1C1、D1C1的中点,求证 (1)E、F、G、H四点共面 (2)平面AEF∥平面BDHG 试题详情
试题详情
2、如图,△ABC为正三角形,EC⊥平面ABC,BD∥CE,且CE=CA=2BD,M是EA的中点,求证 (1)DM∥平面ABC
(2)DE=DA 试题详情
3、如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥面ABCD,PD=DC,E是PC的中点,EF⊥PB于F,求证PA∥平面EDB,PB⊥平面EFD 试题详情
试题详情
4、已知PA⊥平面ABCD,ABCD是矩形,M、N为AB、PC的中点,且PA=AD,求证:平面MND⊥平面PDC 试题详情
5、已知四棱锥P-ABCD底面是边长为a的菱形,且∠ABC=1200,又PC⊥平面AC,PC=h,问在棱PA上是否存在一点E,使平面EBD⊥平面ABCD 试题详情
试题详情
3.2.3空间的角的计算(1)----线线、线面角 [教学目标] [教学重点]异线角与线面角的计算 [教学难点]异线角与线面角的计算 教学过程 一、创设情景 试题详情
三、情感态度和价值观:体会转化的功能
试题详情
试题详情
试题详情
解1:(几何法)作平行线构造两条异面直线所成的角 试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
解3:(坐标法)设正方体棱长为4,以 为正交基底,建立如图所示空间坐标系 为正交基底,建立如图所示空间坐标系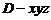 试题详情
试题详情
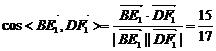
注意:两向量的夹角为锐角或直角时是两条直线的成角,为钝角时为两向量成角的补角 练习:教材P96----练习1,2 试题详情
练习2:在三棱锥S―ABC中,∠SAB=∠SAC=∠ACB=90°,AC=2,BC= ,SB= ,SB=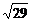  (1)求证:SC⊥BC; 试题详情
(2)求SC与AB所成角的余弦值 试题详情
解:如图,取A为原点,AB、AS分别为y、z轴建立空间直角坐标系,则有AC=2,BC= ,SB= ,SB= , , 试题详情
试题详情
试题详情
(1)∵ ? ? =0,∴SC⊥BC =0,∴SC⊥BC (2)设SC与AB所成的角为α, 试题详情
试题详情
∴cosα= ,即为所求 ,即为所求 试题详情
试题详情
 解:设正方体棱长为1,以 解:设正方体棱长为1,以 为单位正交基底,建立如图所示坐标系D-xyz 为单位正交基底,建立如图所示坐标系D-xyz
试题详情
 为D1AC平面的法向量, 为D1AC平面的法向量,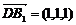
试题详情
试题详情
 所以直线E1F与平面D1AC所成角的余弦值为 所以直线E1F与平面D1AC所成角的余弦值为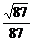
试题详情
试题详情
1、求两直线角的方法:求两直线方向向量成角,若为锐角或直角就是两直线的成角;为钝角时,为两向量成角的补角 试题详情
2、求线面成角的方法:求直线与平面的法向量的成角θ,|θ-900|为所求. [补充习题]已知棱长为1的正方体ABCD-A1B1C1D1中,E为AB的中点,P为正方体对角线A1C上任意一点,求直线A1C与平面PEB1成角正弦值的范围 试题详情
四、布置作业:教材P97----6,7,8,9,11,12 [答案]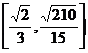 试题详情
3.2.2空间的角的计算(2)――二面角的求法 [教学目标] [教学重点]二面角的计算 [教学难点]二面角的计算 [教学过程] 一、创设情景 试题详情
三、情感态度与价值观:体会问题的转化技能
试题详情
试题详情
原理:一个二面角的平面角 1与这个二面角的两个半平面的法向量所成的角 1与这个二面角的两个半平面的法向量所成的角 2相等或互补。 2相等或互补。 二、建构数学 利用向量求二面角的大小。 试题详情
 方法一:转化为分别是在二面角的两个半平面内且与棱都垂直的两条直线上的两个向量的夹角(注意:要特别关注两个向量的方向)如图:二面角α-l-β的大小为θ, 方法一:转化为分别是在二面角的两个半平面内且与棱都垂直的两条直线上的两个向量的夹角(注意:要特别关注两个向量的方向)如图:二面角α-l-β的大小为θ,
试题详情
试题详情
 方法二:先求出二面角一个面内一点到另一个面的距离及到棱的距离, 方法二:先求出二面角一个面内一点到另一个面的距离及到棱的距离,
然后通过解直角三角形求角。 如图:已知二面角α-l-β,在α内取一点P, 过P作PO⊥β,及PA⊥l,连AO,则AO⊥l成立,∠PAO就是二面角的平面角 试题详情
用向量可求出|PA|及|PO|,然后解三角形PAO  求出∠PAO。 求出∠PAO。 方法三:转化为求二面角的两个半平面的法向量夹角的补角。 如图(1)P为二面角α-l-β内一点,作PA⊥α, PB⊥β,则∠APB与二面角的平面角互补。 三、数学运用 试题详情
试题详情
解:设正方体棱长为1,以 为单位正交基底, 为单位正交基底, 建立如图所示坐标系D-xyz 试题详情
(法一) , ,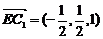 试题详情
试题详情
试题详情
试题详情
例4 、已知E,F分别是正方体 的棱BC和CD的中点,求: 的棱BC和CD的中点,求: (1)A1D与EF所成角的大小; (2)A1F与平面B1EB所成角的大小; 试题详情
(3)二面角 的大小。 的大小。 试题详情
 解:设正方体棱长为1,以 解:设正方体棱长为1,以 为单位正交基底,建立如图所示坐标系D-xyz 为单位正交基底,建立如图所示坐标系D-xyz
试题详情
(1)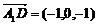 试题详情
试题详情
试题详情
A1D与EF所成角是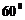 试题详情
(2) , ,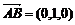 试题详情
试题详情
试题详情
二面角 的正弦值为 的正弦值为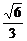 练习:教材:P97---练习4,5 四、回顾总结 试题详情
试题详情
2、法向量的夹角与二面角相等或互补的判断: 五、布置作业:教材P97---98习题3,5,10,13 [补充习题] 试题详情
1、空间一点P到二面角α-l-β的两个面α、β及棱l的距离分别为 、 、 、2,则这个二面角的大小为_______ 、2,则这个二面角的大小为_______ 试题详情
2、如图在长方体ABCD-A1B1C1D1中,已知AB=4,AD=3,AA1=2,E、F分别是线段AB、BC上的点,且EB=FB=1 ⑴求二面角C-DE-C1的正切值;⑵求直线EC1与FD1所成角的余弦值 试题详情
3、在正四棱柱ABCDF-A1B1C1D1中,侧棱是底面边长的2倍,P是CC1上的任意一点 ⑴求证:总有BD⊥AP;⑵若CC1=3C1P,求平面AB1P与平面ABCD所成的二面角的余弦值;⑶当点P在CC1上何处时,AP在平面B1AC上的射影是∠B1AC的平分线 [答案] 试题详情
试题详情
2、⑴ ;⑵ ;⑵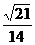 试题详情
3、⑴略;⑵ ;⑶PC= ;⑶PC= CC1 CC1
知识汇总 一、基本结论 空间向量是由平面向量推广而来,所以空间向量中的许多结论与平面向量有类似结论 试题详情
试题详情
试题详情
试题详情
4、数量积: = = = a1a2+b1b2+c1c2 = a1a2+b1b2+c1c2 二、应用 试题详情
试题详情
⑴直线与直线:两直线a,b的方向向量分别为 、 、 , , 试题详情
试题详情
试题详情
⑵直线与平面:直线a的方向向量为 ,平面α的法向量为 ,平面α的法向量为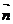 试题详情
试题详情
试题详情
⑶平面与平面:平面α、β法向量分别为 、 、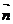 试题详情
试题详情
试题详情
试题详情
试题详情
⑵直线与平面的成角:设直线a的方向向量为 ,平面α大法向量为 ,平面α大法向量为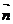 ,则a与α的成角为 ,则a与α的成角为 试题详情
| | | 试题详情
⑶二面角的平面角:二面角α-l-β的平面角为θ,α、β的法向量分别为 、 、 试题详情
若在α、β内分别存在OA⊥l,OB⊥l,O为l上一点,则θ=< > > 试题详情
θ与< , , >相等或互补 >相等或互补 练习:教材复习题11,12 作业:复习题1~10 试题详情
| 
 上的向量
上的向量 以及与
以及与 共线的向量叫做直线
共线的向量叫做直线 的方向向量
的方向向量 的有向线段所在直线垂直于平面α,则称这个向量垂直于平面α,记作
的有向线段所在直线垂直于平面α,则称这个向量垂直于平面α,记作 ,如果
,如果 ,那么向量
,那么向量 叫做平面α的法向量。
叫做平面α的法向量。 中,求证:
中,求证: 是平面
是平面 的法向量
的法向量 证:设正方体棱长为1,以
证:设正方体棱长为1,以 为单位正交基底,
为单位正交基底,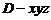
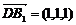 ,
, ,
,
 ,所以
,所以

 平面
平面
 经过点
经过点 ,平面
,平面 的法向量为
的法向量为 ,
, 为平面
为平面 内任意一点,求
内任意一点,求 满足的关系式。
满足的关系式。
 即
即

 是平面ABC的一个法向量,且|
是平面ABC的一个法向量,且| |=
|= ,求
,求 ;(3)求平面ABC满足的方程
;(3)求平面ABC满足的方程

 是平面BED的法向量
是平面BED的法向量 ,
, >
> ,
, ,1) (2)(-
,1) (2)(- ,1,-1)
,1,-1) a (2)-
a (2)-
 的方向向量分别为
的方向向量分别为 ,两个平面
,两个平面 的法向量分别为
的法向量分别为 ,则由如下结论
,则由如下结论 与
与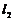


 与
与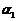


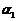 与
与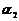

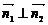
 已知:如图,OB是平面
已知:如图,OB是平面 的斜线,O为斜足,
的斜线,O为斜足, ,A为垂足,
,A为垂足,







 ,
,

 内任作一条直线
内任作一条直线 ,在直线
,在直线 上分别取向量
上分别取向量







 例3 在直三棱柱
例3 在直三棱柱 中,
中, ,
,  ,
, 是
是 得中点。求证:
得中点。求证: (教材88页例3)
(教材88页例3)


 )
)