
题目列表(包括答案和解析)
20.(本小题满分12分)
如图,在棱长为1的正方体ABCD-A1B1C1D1中,
(1)线段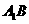 上是否存在一点
上是否存在一点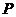 使得
使得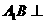 平面
平面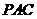 ,若存在,确定
,若存在,确定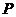 点的位置,若不存在,说明理由;
点的位置,若不存在,说明理由;
(2)点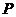 在线段
在线段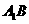 上,若二面角
上,若二面角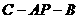 的大小是
的大小是 ,求
,求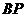 的长;
的长;
(3)点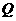 在对角线
在对角线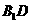 上,使
上,使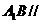 平面
平面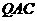 ,求
,求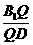 。
。

19.(本小题满分12分)
设函数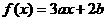 (常数
(常数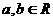 且
且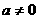 )的定义域是
)的定义域是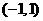 。如果对于定义域内的每一个
。如果对于定义域内的每一个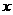 ,都有
,都有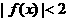 ,那么
,那么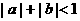 。
。
(1)证明上述命题;
(2)写出上述命题的逆命题。若逆命题正确,请加以证明;若逆命题不正确,请举出一个反例说明。
18.(本小题满分12分)
设棋子在正四面体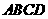 的表面从一个顶点移向另外三个顶点是等可能的。现抛掷骰子根据其点数决定棋子是否移动:若投出的点数是奇数,则棋子不动;若投出的点数是偶数,棋子移动到另一顶点。若棋子的初始位置在顶点
的表面从一个顶点移向另外三个顶点是等可能的。现抛掷骰子根据其点数决定棋子是否移动:若投出的点数是奇数,则棋子不动;若投出的点数是偶数,棋子移动到另一顶点。若棋子的初始位置在顶点 ,回答下列问题。
,回答下列问题。

(1)投了2次骰子,棋子才到达顶点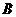 的概率是多少?
的概率是多少?
(2)投了3次骰子,棋子恰巧在顶点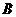 的概率是多少?
的概率是多少?
17.(本小题满分12分)
函数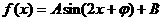 (其中
(其中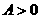 、
、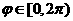 )的图像经过三点
)的图像经过三点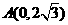 、
、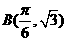 、
、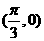 。
。
(1)求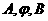 的值;
的值;
(2)是否存在常数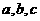 ,使
,使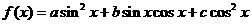 恒成立?若存在,求出
恒成立?若存在,求出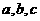 ,若不存在,说明理由。
,若不存在,说明理由。
16.某工厂生产A、B、C三种不同型号的产品,产品数量之比依次为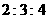 ,现用分层抽样方法抽出一个容量为
,现用分层抽样方法抽出一个容量为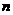 的样本,样本中A种型号产品有16件.那么此样本的容量
的样本,样本中A种型号产品有16件.那么此样本的容量 =
。
=
。
15.
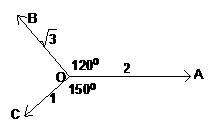
如图,向量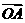 、
、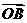 、
、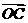 的长度分别是2、
的长度分别是2、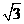 、1,
、1,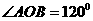 、
、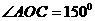 ,则
,则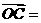
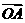 +
+ 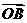 。
。
14.凸多面体是由4个三角形和5个四边形围成,则其顶点数是 。
13.不等式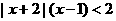 的解集是
。
的解集是
。
12.若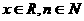 ,定义:
,定义: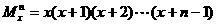 ,例如:
,例如: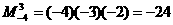 ,则函数
,则函数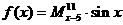 的奇偶性是( )
的奇偶性是( )
A.是偶函数不是奇函数 B.是奇函数不是偶函数
C.既是奇函数又是偶函数 D.既不是奇函数又不是偶函数
第Ⅱ卷(共90分)
11.定义在区间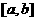 (
(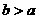 )上的函数
)上的函数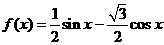 的值域是
的值域是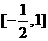 ,则
,则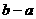 的最大值
的最大值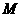 和最小值
和最小值 分别是( )
分别是( )
A.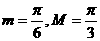 B.
B.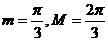
C.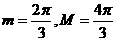 D.
D.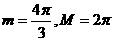
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com