
题目列表(包括答案和解析)
4.已知函数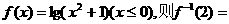 ( )
( )
A.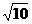 B.-
B.-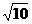 C.3
C.3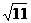 D.-3
D.-3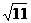
3.(理科)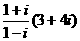 = ( )
= ( )
A.-4+3i B.-4-3i C.4+3i D.4-3i
(文科)为了得到函数y=cos(2x+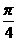 )的图象,可以将函数y=sin(2x+
)的图象,可以将函数y=sin(2x+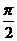 )的图象( )
)的图象( )
A.向左平移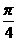 个单位长度 B.向左平移
个单位长度 B.向左平移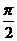 个单位长度
个单位长度
C.向右平移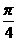 个单位长度 D.向右平移
个单位长度 D.向右平移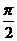 个单位长度
个单位长度
2.已知函数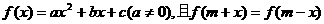 ,则m等于 ( )
,则m等于 ( )
A.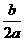 B.-
B.-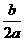 C.
C. D.-
D.-
1.已知集合A,B,I,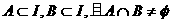 .则下面关系式正确的是 ( )
.则下面关系式正确的是 ( )
A.(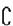 IA)∪(
IA)∪(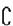 IB)=I B.(
IB)=I B.(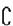 IA)∪B=I
IA)∪B=I
C.A∪B=I D.(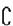 I(A∩B))∪(A∩B)=I
I(A∩B))∪(A∩B)=I
7.3 若干应用题
(1) 某罐装饮料厂为降低成本要将制罐材料减少到最小,假设罐装饮料筒为圆柱体(视上、下底为平面),上下底半径为r,高为h,若体积为V,上下底厚度分别是侧面厚度的2倍,试问当r与h之比是多少时用料最少?
(2)
商店经销某种商品,年销售量为D件,每件商品库存费用为I元,每批进货量为Q件,每次进货所需费用为S元,现假设商店卖完该货物时立即进货,使库存量为平均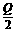 件,问每批进货件数Q为多大时,整个费用最省?
件,问每批进货件数Q为多大时,整个费用最省?
(3) 某轮船公司争取到一个相距1000海里的甲、乙两地的客运航线权.已知轮船限载人数为400人,轮船每小时使用的燃料费用和轮船速度的立方成正比例,轮船的最大时速是25海里/时,当船速为10海里/时,它的燃料费用是每小时30元,其余费用(不论速度如何)都是每小时480元.你能为该公司设计一种较为合理的船票价格吗?
(4) 为了确保交通安全,交通部门规定:某事故易发地段内的车距d正比于车速v(千米/时)的平方与车身长(米)的积,且最小车距不得少于半个车身长.假定车身长均为s(米),且车速为50(千米/时)时,车距恰为车身长S.问交通繁忙时,应规定怎样的车速,才能使此地段车流量Q最大?
(5)
铁道车运行1小时所需的成本由两部分组成,固定部分m元,变动部分与运行速度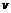 (千米/时)的平方成正比例,比例系数为 k(k>0),如果机车匀速从甲站开往乙站,为使成本最省,应以怎样的速度运行?
(千米/时)的平方成正比例,比例系数为 k(k>0),如果机车匀速从甲站开往乙站,为使成本最省,应以怎样的速度运行?
(6) 某罐装饮料厂为降低成本要将制罐材料减少到最小,假设罐装饮料筒为正圆柱体(视上、下底为平面),上、下底半径为r,高为h.若体积为V,上、下底厚度分别是侧面厚度的2倍,试问当r与h之比是多少时用料最少?
(7) 商店经销某种货物,年销售量是5万件.因集装运输要求,这批货物可分为若干次等量进货,每次运费500元.商店进货后,需人库暂存,销售完后可立即进货.仓库年租金按最大储存量时每件4元收费(以后不超量的各次货物进出不再收费),为尽量减少运费和库存费总开支,每次进货应是多少件?全年运费和库存费总开支最少多少元?
(8) 在半径为R的球内挖去一个以球的直径为轴的圆柱型孔.当孔的面积(即圆柱的侧面积)最大时,球套在杆上不易打滑,此时的孔半径为多少?
(9) 要建造一个底面为正方形,容量为32m3的柱形露天水池.(A)问水池尺寸如何选取,才能使所用材料最省?(B) 若池底材料成本30元/m2,池壁材料成本为20元/m2,问选取怎样的尺寸,水池造价最低?
(10) 已知圆柱的表面积为S , 求圆柱体积V的最大值.
(11)
已知一个长方体的长、宽、高之和等于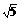 ,求它的体积的最大值.
,求它的体积的最大值.
(12) 圆锥底面半径为R,高为H,求它内接圆柱的最大体积。
(13)
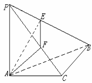
如图,已知直线角三角形ABC的斜边为AB,过A作AP 平面ABC,
平面ABC,
AE PB交PB于E,AF
PB交PB于E,AF PC交PC于F,① 求证:PB
PC交PC于F,① 求证:PB 平面
平面
AEF;② 设AP=AB=2,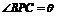 是变量,求四面体PAEF体积的
是变量,求四面体PAEF体积的
最大值,并求出这时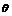 的值.
的值.
7.2 在解析几何中的应用
(1)
过点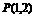 作直线
作直线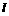 与
与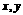 轴正方向交于
轴正方向交于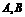 两点,
两点,
①当△ 面积最小时,求直线
面积最小时,求直线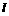 的方程.
的方程.
②当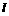 在两轴上截距之和最小时,求直线
在两轴上截距之和最小时,求直线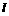 的方程.
的方程.
③当 最小时,求直线
最小时,求直线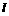 的方程.
的方程.
(2)
在直线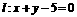 上求一点
上求一点 使点
使点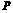 对
对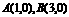 的张角最大.
的张角最大.
(3)
已知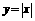 的图象中,有一长为定值
的图象中,有一长为定值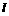 的线段
的线段 的端点分别在两条射线上移动.
的端点分别在两条射线上移动.
①求 的中点的轨迹方程.
的中点的轨迹方程.
②设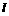 方程为
方程为 ,求
,求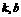 的关系.
的关系.
③当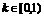 时,求
时,求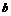 的取值范围.
的取值范围.
(4)
定长为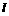 的线段
的线段 两端点在抛物线
两端点在抛物线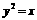 上移动.求动点
上移动.求动点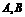 的中点
的中点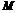 的轨迹方程.
的轨迹方程.
求离 轴最近的中点
轴最近的中点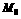 的坐标.
的坐标.
7.1 求下列函数的值域或最值
(1)
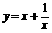
 .
.
(2) 若下面各式中字母均为正数
① 求 的最大值. ② 求x +
的最大值. ② 求x +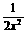 的最小值. ③ 当log4x+log4y=2时, 求
的最小值. ③ 当log4x+log4y=2时, 求 的最小值.
的最小值.
(3)
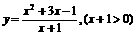
(4)
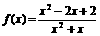
(5)
点 在直线
在直线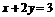 上, 求
上, 求 的最小值.
的最小值.
5. 数形结合法
求下列函数的值域
(1)

(2)
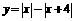
(3)
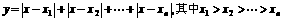
(4)
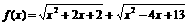
(5)

(6)
已知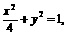 求
求 的最大值和最小值.
的最大值和最小值.
(7)
对于任意实数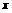 ,设函数
,设函数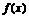 是
是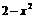 与
与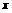 中较小者,求
中较小者,求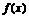 的最大值.
的最大值.
方法的综合
求函数 的最大值.
的最大值.
6. 已知函数的值域求参数的值
(1) 已知函数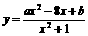 的值域是
的值域是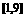 ,求
,求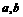 的值.
的值.
(2) 已知函数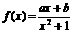 的值域是
的值域是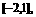 求
求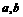 的值.
的值.
7. 函数的值域与均值不等式
4.反解法(反函数法)
求下列函数的值域
(1)
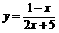
(2)

(3)

(4)
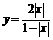
(5)
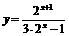
(6)
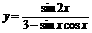
(7)
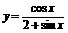
(8)


3. 函数单调性法
求下列函数的值域
(1)
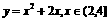
(2)
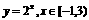
(3)
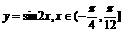
(4)
已知二次函数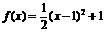 的定义域和值域都为
的定义域和值域都为 ,求b的值.
,求b的值.
(5)

(6)

(7)
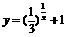
(8)
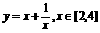
(9)
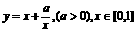
(10) 函数 在区间
在区间 上的最大值与最小值之差为1,求a的值.
上的最大值与最小值之差为1,求a的值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com