
题目列表(包括答案和解析)
3.“0<x<5”是“不等式|x-2|<3”成立的 ( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.不充分不必要条件
2. ( )
( )
A.0 B.1 C.2 D.3
一项是符合题目要求的.
1.函数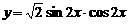 是
( )
是
( )
A.周期为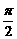 的奇函数 B.周期为
的奇函数 B.周期为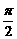 的偶函数
的偶函数
C.周期为 的奇函数 D.周期为
的奇函数 D.周期为 的偶函数
的偶函数
22.(1)以O为原点,OA所在的直线为x轴建立如图所示的直角坐标系,
则A(2,0),设所求椭圆的方程为: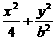 =1(0<b<2),由椭圆的对称性知|OC|=|OB|,
=1(0<b<2),由椭圆的对称性知|OC|=|OB|,
由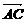 ·
·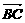 =0得AC⊥BC,
=0得AC⊥BC,
∵|BC|=2|AC|,∴|OC|=|AC|,∴△AOC是等腰直角三角形,∴C的坐标为(1,1),
∵C点在椭圆上
∴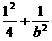 =1,∴b2=
=1,∴b2=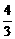 ,所求的椭圆方程为
,所求的椭圆方程为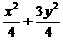 =1.
…………6分
=1.
…………6分
(2)由于∠PCQ的平分线垂直OA(即垂直于x轴),不妨设直线PC的斜率为k,则直线QC的斜率为-k,直线PC的方程为:y=k(x-1)+1,直线QC的方程为y=-k(x-1)+1, ………………8分
由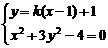 得:(1+3k2)x2-6k(k-1)x+3k2-6k-1=0(*) …………10分
得:(1+3k2)x2-6k(k-1)x+3k2-6k-1=0(*) …………10分
∵点C(1,1)在椭圆上,∴x=1是方程(*)的一个根,则其另一根为 ,设P(xP,yP),?Q(xQ,yQ),xP=
,设P(xP,yP),?Q(xQ,yQ),xP= ,
,
同理xQ= ,
…………12分
,
…………12分
kPQ=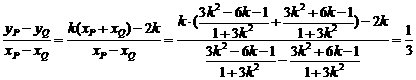
而由对称性知B(-1,-1),又A(2,0),
∴kAB=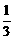 ,
,
∴kPQ=kAB,∴ 与
与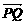 共线,且
共线,且 ≠0,即存在实数λ,使
≠0,即存在实数λ,使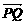 =λ
=λ . ………14分
. ………14分
21.(1)由已知得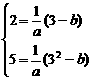 解得
解得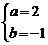 …………2分
…………2分
∴f(x)=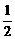 (3x+1)
…………4分
(3x+1)
…………4分
令y=f(x),由y=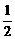 (3x+1)得3x=2y-1,∴x=log3(2y-1),
(3x+1)得3x=2y-1,∴x=log3(2y-1),
∴f-1(x)=log3(2x-1)(x>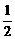 ).
…………6分
).
…………6分
(2)an=3log3(2n-1)=2n-1,n∈N* …………8分
设存在正数k,使(1+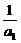 )(1+
)(1+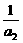 )…(1+
)…(1+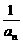 )≥k
)≥k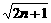 成立,
成立,
则k≤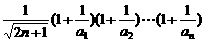 ,
,
记F(n)= 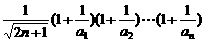 ,则
,则
F(n+1)=
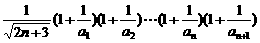 ,
,
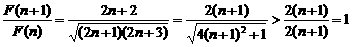
∴F(n+1)>F(n),
∴F(n)是随n的增大而增大, …………10分
∵n∈N*,∴当n=1时,F(n)min=F(1)=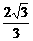 ,
,
∴k≤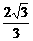 ,即k的最大值为
,即k的最大值为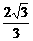 .
…………12分
.
…………12分
20.(1)V=4(a-x)2•x,定义域为(0,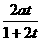 );
);
(2)当t≥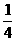 时,x=
时,x=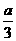 ,V取最大值;当0<t<
,V取最大值;当0<t<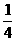 时,x=
时,x=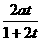 ,V取最大值.
,V取最大值.
19.(1)
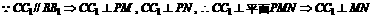 ;
;
(2) 在斜三棱柱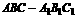 中,有
中,有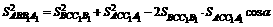 ,其中
,其中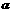 为平面
为平面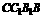 与平面
与平面 所组成的二面角.
所组成的二面角.
 上述的二面角为
上述的二面角为 ,在
,在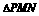 中,
中,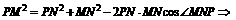
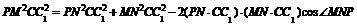 ,
,
由于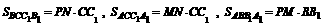 ,
,
 有
有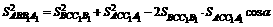 .
.
18.(1)依题意,随机变量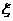 的取值是2、3、4、5、6.…………2分
的取值是2、3、4、5、6.…………2分
因为P(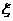 =2)=
=2)=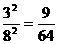 ;P(
;P(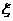 =3)=
=3)=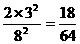 ,
,
P(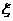 =4)=
=4)=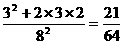 ;P(
;P(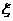 =5)=
=5)=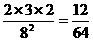 ;
;
P(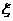 =6)=
=6)=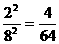 ;…………7分
;…………7分
所以,当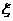 =4时,其发生的概率P(
=4时,其发生的概率P(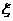 =4)=
=4)=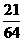 最大.…………8分
最大.…………8分
(Ⅱ)E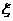 =
= .………………12分
.………………12分
17.依题意有, +
+ =
=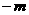 ,
,
 =
=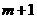 ,
,

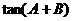 =
=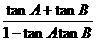 =
=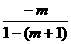 =1.…………..3分
=1.…………..3分

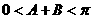 ,
,
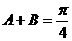 .从而
.从而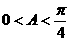 ,
,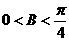 ,
,
故
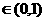 ,
,
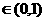 .…………..6分
.…………..6分
即方程 的两个实根均在
的两个实根均在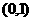 内.
内.
设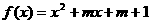 ,
,
则函数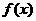 与
与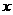 轴有两个交点,且交点在
轴有两个交点,且交点在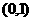 内;
内;
又函数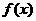 的图象是开口向上的抛物线,且对称轴方程为
的图象是开口向上的抛物线,且对称轴方程为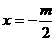 ,
,
故其图象满足
 即
即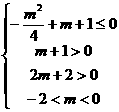 …………..9分
…………..9分
解之,得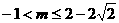 ,
,
故所求 的范围是
的范围是 .…………..12分
.…………..12分
16.取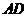 的中点
的中点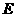 ,连结
,连结 ,
,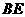 ;得三棱锥外接球的半径为
;得三棱锥外接球的半径为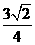 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com