
题目列表(包括答案和解析)
22.(本小题满分14分)
设函数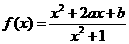 ,其中
,其中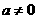 ,
,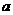 、
、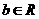 .
.
(Ⅰ)若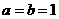 ,求函数
,求函数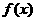 的值域;
的值域;
(Ⅱ)存在实数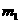 、
、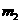 (
(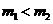 )满足等式
)满足等式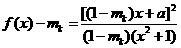 ,(
,(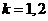 );
);
(Ⅲ)对于(Ⅱ)中的实数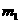 、
、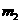 ,有
,有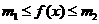 成立.
成立.
21.(本小题满分14分)
如图,曲线C是顶点在原点,以x轴为对称轴开口向右的抛物线,点M(2,1)到抛物线准线的距离为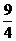 。
。
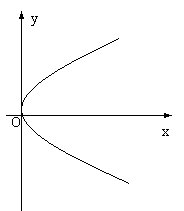 (1)求抛物线C的方程;
(1)求抛物线C的方程;
(2)若直线l过抛物线上P、Q不同两点,且与x轴
交于点T,与y轴交于点S,求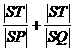 的取值范围;
的取值范围;
(3)若过点M的直线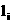 (i=1,2,3,4)分别与抛物线
(i=1,2,3,4)分别与抛物线
C交于上下两点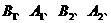
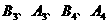 ,
,
又点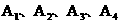 的纵坐标依次成公差不为零的等差数列,
的纵坐标依次成公差不为零的等差数列,
试分析推导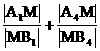 与
与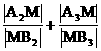 的大小.
的大小.
19.(本小题满分12分)
如图,在棱长为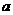 的正方体ABCD-A1B1C1D1中,EF分别为棱AB和BC的中点,EF交BD于H。
的正方体ABCD-A1B1C1D1中,EF分别为棱AB和BC的中点,EF交BD于H。
(1)求二面角B1-EF-D的正切值;(2)设M为BB1中点,求证D1M⊥平面EFB1;
 (3)求点D到平面EFB1的距离。
(3)求点D到平面EFB1的距离。
20(本小题满分12分)
已知函数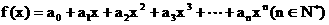 , 且
, 且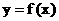
的图象经过点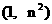 , 数列
, 数列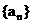 为等差数列.
为等差数列.
(1)
求数列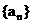 的通项公式
的通项公式
(2) 当n为奇数时, 设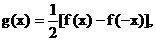 试求
试求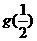
18.(本小题满分12分)
设向量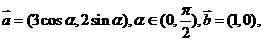
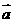 与
与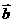 的夹角为
的夹角为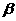
(1)求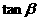 (用
(用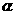 表示)
表示)
(2) 试求 的最大值及对应的
的最大值及对应的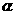 值。
值。
17.(本小题满分10分)
多向飞碟是奥运竞赛项目,它是由跑靶机把碟靶(射击目标)在一定范围内从不同方向飞出,每抛出一个碟靶,都允许运动员射击两次。一运动员进行多向飞碟训练时,每次射击碟靶的概率为p与运动员离碟靶的距离S(m)成反比,现有一碟靶抛出后离运动员的距离S(m)与飞行时间t(s)满足S=15(t+1),.若运动员在碟靶飞出0.5s时进行第一次射击,命中的概率0.8,若他发现没有命中,则在进行第一次射击后过0.5s进行第二次射击,求他命中此靶的概率。
13、 14、 15、 16、① ②
16.已知平面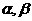 和直线,给出条件:①
和直线,给出条件:①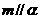 ;②
;②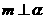 ;③
;③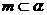 ;④
;④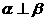 ;⑤
;⑤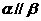 .
.
(i)当满足条件
时,有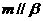 ;(ii)当满足条件
时,有
;(ii)当满足条件
时,有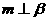 .
.
(填所选条件的序号)
高三数学周练试题(五)
班级_______________ 姓名_________________ 学号________
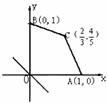
15.给出平面区域如图所示, 目标函数为: 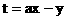
若当且仅当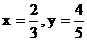 时, 目标函数t取最小值,
时, 目标函数t取最小值,
则实数a的取值范围是 .
14. “渐减数”是指每个数字比其左边数字小的正整数(如98765),若把所有五位渐减数按从小到大的顺序排列,则第55个数为 .
“渐减数”是指每个数字比其左边数字小的正整数(如98765),若把所有五位渐减数按从小到大的顺序排列,则第55个数为 .
13.设直线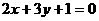 和圆
和圆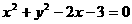 相交于点A、B,则弦AB的垂直平分线方程是
.
相交于点A、B,则弦AB的垂直平分线方程是
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com