
题目列表(包括答案和解析)
4、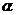 ∩
∩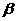 =MN,A∈
=MN,A∈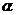 ,C∈MN,且∠ACM=45°,
,C∈MN,且∠ACM=45°,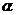 -MN-
-MN-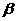 是60°的二面角,AC=1,则点A到平面
是60°的二面角,AC=1,则点A到平面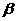 的距离___________.
的距离___________.
3、若三棱锥P-ABC中过点P的三条侧棱两两垂直,长都是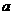 ,则底面上任一点到三个侧面距离之和为___________.
,则底面上任一点到三个侧面距离之和为___________.
2、四棱锥P-ABCD的底面为正方形PD⊥底面ABCD,PD=AD=1,设点C到平面PAB的距离为d1,点B到平面PAC的距离为d2,BC到平面PAD的距离为d3,则有( )
A.d3<d1<d2 B.d1<d2<d3 C.d1<d3<d2 D.d2<d1<d3
1、在正方体ABCD-A1B1C1D1中,AB=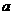 ,M是AA1的中点,则点A1到平面MBD的距离是( )
,M是AA1的中点,则点A1到平面MBD的距离是( )
A.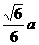 B.
B.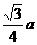
C.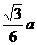 D.
D.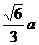
2、各种距离之间的相互转化,等体积法及“平行移动”等思想方法.
基础练习
1、点到平面的距离;
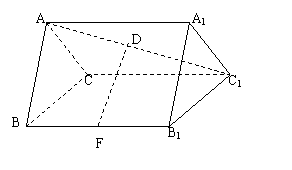
8、如图,在正三棱柱ABC-A1B1C1中,各棱长都等于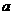 ,D、F分别为AC1和BB1的中点
,D、F分别为AC1和BB1的中点
(1)求证:DF为异面直线AC1和BB1的公垂线段并求其长度;
(2)求点C1到平面AFC的距离.
高三数学教学案 第九章 立体几何
第十五课时 距离(二)
考纲摘录
进一步掌握空间两条直线、直线和平面、两个平面及点到平面距离的求法.
知识概要
7、已知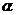 -
-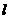 -
-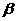 的大小是60°,AB
的大小是60°,AB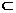
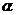 ,CD
,CD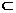
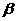 ,并且AB⊥
,并且AB⊥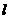 于A,CD⊥
于A,CD⊥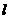 于C,AB=AC=CD=
于C,AB=AC=CD=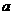 ,求:
,求:
(1)B、D两点间的距离;
(2)点D到AB的距离.
6、已知Rt△ABC的直角顶点C在平面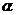 内,斜边AB∥
内,斜边AB∥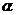 ,AB=
,AB=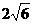 ,AC、BC分别和平面
,AC、BC分别和平面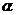 成45°和30°角,求AB到平面
成45°和30°角,求AB到平面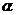 的距离.
的距离.
5、△ABC的三个顶点A、B、C到平面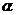 的距离分别为2,3,4,且它们在
的距离分别为2,3,4,且它们在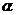 的同侧,则△ABC的重心到平面
的同侧,则△ABC的重心到平面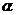 的距离为__________.
的距离为__________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com