
题目列表(包括答案和解析)
1.化简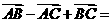 .
.
11.已知函数f(x)定义域为[0,1],且同时满足
(1)对于任意x∈[0,1],且同时满足; (2)f(1)=4;
(3)若x1≥0,x2≥0,x1+x2≤1,则有 f(x1+x2)≥f(x1)+f(x2)-3.
(Ⅰ)试求f(0)的值; (Ⅱ)试求函数f(x)的最大值;
(Ⅲ)设数列{an}的前n项和为Sn,满足a1=1,Sn=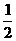 (an-3),n∈N*.
(an-3),n∈N*.
求证:f(a1)+f(a2)+…+f(an)<
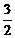 log3
log3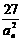 .
.
10. 设抛物线过定点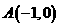 ,且以直线
,且以直线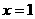 为准线.
为准线.
(Ⅰ)求抛物线顶点的轨迹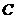 的方程;
的方程;
(Ⅱ)若直线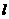 与轨迹
与轨迹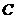 交于不同的两点
交于不同的两点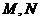 ,且线段
,且线段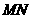 恰被直线
恰被直线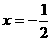 平分,设弦MN的垂直平分线的方程为
平分,设弦MN的垂直平分线的方程为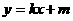 ,试求
,试求 的取值范围.
的取值范围.
9. 已知两点M(-2,0),N(2,0),动点P(x,y)在y轴上的射影为H,|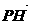 |是2和
|是2和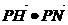 的等比中项.
的等比中项.
(1)求动点P的轨迹方程;
(2)若以点M、N为焦点的双曲线C过直线x+y=1上的点Q,求实轴最长的双曲线C的方程.
8. 设数列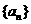 是首项为6,公差为1的等差数列;
是首项为6,公差为1的等差数列;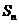 为数列
为数列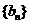 的前
的前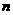 项和,且
项和,且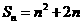
(1)求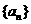 及
及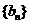 的通项公式
的通项公式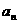 和
和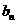 ;
;
(2)若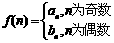 ,问是否存在
,问是否存在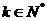 使
使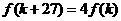 成立?若存在,求出
成立?若存在,求出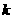 的值;若不存在,说明理由;
的值;若不存在,说明理由;
(3)若对任意的正整数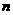 ,不等式
,不等式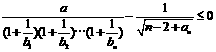 恒成立,求正数
恒成立,求正数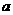 的取值范围。
的取值范围。
7.设函数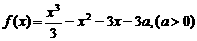 .
.
(Ⅰ)如果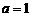 ,点P
,点P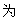 曲线
曲线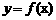 上一个动点,求以P为切点的切线其斜率取最小值时的切线方程;
上一个动点,求以P为切点的切线其斜率取最小值时的切线方程;
(Ⅱ)若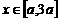 时,
时,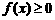 恒成立,求
恒成立,求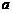 的取值范围.
的取值范围.
6. 数列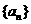 的前项
的前项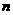 和记为
和记为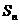 ,数列
,数列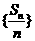 是首项为2,公比也为2的等比数列.
是首项为2,公比也为2的等比数列.
(Ⅰ)求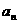 ;(Ⅱ)若数列
;(Ⅱ)若数列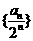 的前
的前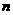 项和不小于100,问此数列最少有多少项?
项和不小于100,问此数列最少有多少项?
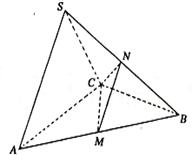
5. 在三棱锥S-ABC中,△ABC是边长为4的正三角形,
平面SAC⊥平面ABC,SA=SC=2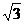 ,M、N分别为AB、SB的中点.
,M、N分别为AB、SB的中点.
(1)证明:AC⊥SB;
(2)求二面角N-CM-B的大小;
(3)求点B到平面CMN的距离.
4、如图,四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,PA=PB=1,AD=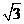 ,点F是PB的中点,点E在边BC上移动。
,点F是PB的中点,点E在边BC上移动。
 (1)求三棱锥E-PAD的体积;
(1)求三棱锥E-PAD的体积;
(2)点E为BC的中点时,试判断EF与平面PAC的位置关系,并说明理由;
(3)证明:无论点E在BC边的何处,都有PE⊥AF;
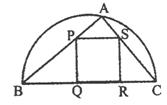
3. 某园林单位准备绿化一块直径为BC的半圆形空地,△ABC外的地方种草,△ABC的内接正方形PQRS为一水池,其余的地方种花。若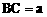 ,∠ABC=θ,设△ABC的面积为S1,正方形的面积为S2。
,∠ABC=θ,设△ABC的面积为S1,正方形的面积为S2。
(1)用a,θ表示S1和S2;
 (2)当a固定,θ变化时,求
(2)当a固定,θ变化时,求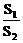 取最小值时的角θ。
取最小值时的角θ。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com