
题目列表(包括答案和解析)
3.设函数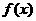 ,对于任意实数
,对于任意实数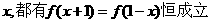 ,且方程
,且方程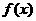 =0有2007个解,则这2007个解之和为( )
=0有2007个解,则这2007个解之和为( )
A.0 B.-1 C.2007 D.4014。
2.已知等差数列{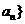 中,
中,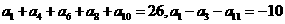 ,则
,则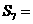 ( )
( )
A.20 B.22 C.26 D.28
1.复数Z=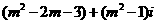 为纯虚数,则实数m= ( )
为纯虚数,则实数m= ( )
A.-1.or.3 B.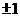 C.3 D.1
C.3 D.1
21.(本小题满分14分)已知函数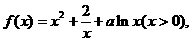
(1) 若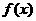 在
在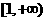 上单调递增,求
上单调递增,求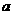 的取值范围;
的取值范围;
(2) 若定义在区间D上的函数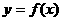 对于区间D上的任意两个值
对于区间D上的任意两个值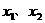 总有以下不等式
总有以下不等式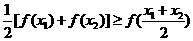 成立,则称函数
成立,则称函数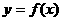 为区间D上的“凹函数”.
为区间D上的“凹函数”.
试判断当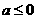 时,
时,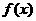 是否为“凹函数”,并对你的判断加以证明.
是否为“凹函数”,并对你的判断加以证明.
解:(Ⅰ)由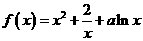 ,得
,得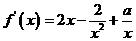 ……………………2分
……………………2分
欲使函数为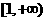 上单调增函数,则
上单调增函数,则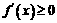 在
在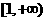 上恒成立,即不等式
上恒成立,即不等式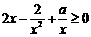 在
在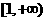 上恒成立.也即
上恒成立.也即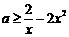 在
在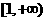 上恒成立.………………4分
上恒成立.………………4分
令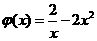 ,上述问题等价于
,上述问题等价于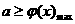 ,而
,而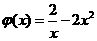 为在
为在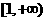 上的减函数,则
上的减函数,则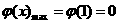 ,于是
,于是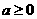 为所求. ………………………………………………6分
为所求. ………………………………………………6分
(Ⅱ)证明:由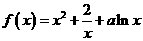 得
得
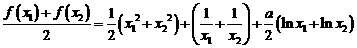
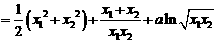 ………………………………7分
………………………………7分
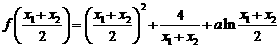 ………………………………………8分
………………………………………8分
而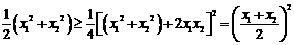 ① ………………………10分
① ………………………10分
又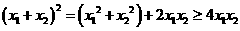 , ∴
, ∴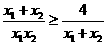 ② …………11分
② …………11分
∵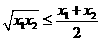 ∴
∴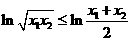 ,
,
∵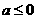 ∴
∴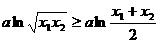 ③ …………………………………13分
③ …………………………………13分
由①、②、③得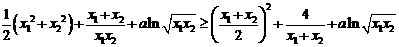
即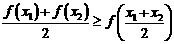 ,
,
从而由凹函数的定义可知函数为凹函数. …………14分
湖南省部分中学2007年4月高三调研联考数学理科
本试题分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。共150分。考试时间120分钟。
第Ⅰ卷(选择题,共50分)
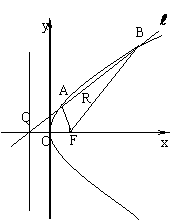
20.(本小题满分13分)
如图, 是抛物线
是抛物线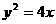 的焦点,
的焦点,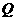 是准线与
是准线与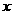 轴的交点,直线
轴的交点,直线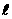 经过点
经过点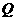 。
。
(1)
直线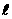 与抛物线有唯一公共点,求
与抛物线有唯一公共点,求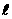 的方程;
的方程;
(2)
直线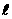 与抛物线交于A,B两点,
与抛物线交于A,B两点,
(Ⅰ)记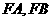 的斜率分别为
的斜率分别为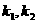 ,求
,求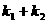 的值;
的值;
(Ⅱ)若点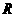 在线段
在线段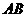 上,且满足
上,且满足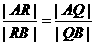 ,求点
,求点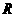 的轨迹方程。
的轨迹方程。
解: 依题意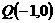 ,直线
,直线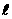 斜率存在,设其斜率为
斜率存在,设其斜率为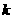 ,则
,则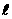 的方程为
的方程为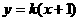 ,代入抛物线方程有:
,代入抛物线方程有: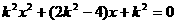 ……………2分
……………2分
(1)若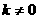 ,令
,令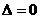 得,
得,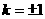 ,此时,
,此时,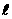 的方程为
的方程为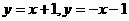 。…………………4分
。…………………4分
若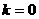 ,方程有唯一解。此时方程为
,方程有唯一解。此时方程为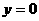 ………5分
………5分
(2)显然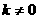 ,记
,记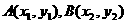 ,
,
则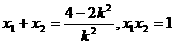 ,
,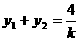 ,
,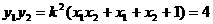 ………7分
………7分
(Ⅰ)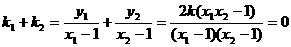 ………………………9分
………………………9分
(Ⅱ)设点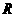 的坐标为
的坐标为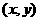 ,∵
,∵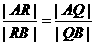 ,∴
,∴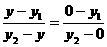 ,
,
∴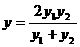 …………………11分 ∴
…………………11分 ∴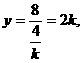
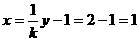 ,………12分
,………12分
由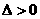 得,
得, ,又
,又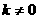 ,∴
,∴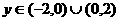 。
。
综上,点R的轨迹方程为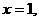
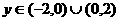 。…………………………13分
。…………………………13分
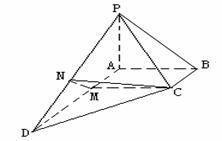
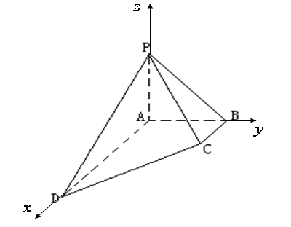
19.
(本小题满分12分)如图,在四棱锥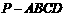 中,侧棱PA⊥底面ABCD, AD∥BC,∠ABC=
中,侧棱PA⊥底面ABCD, AD∥BC,∠ABC=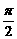 ,
,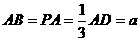 ,
,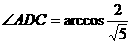 .
.
(Ⅰ) 求点D到平面PBC的距离; (Ⅱ) 求二面角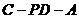 的大小.
的大小.
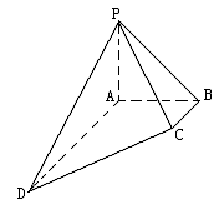
解:(Ⅰ)如图,在四棱锥 中,
中,
∵BC∥AD,从而点D到平面PBC间的距离等于点A到平面PBC的距离.
∵∠ABC=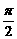 ,∴AB⊥BC, 又PA⊥底面ABCD,∴PA⊥BC,
,∴AB⊥BC, 又PA⊥底面ABCD,∴PA⊥BC,
∴BC⊥平面 PAB,………………2分
∴平面PAB⊥平面PBC,交线为PB,过A作AE⊥PB,垂足为E,则AE⊥平面PBC,
∴AE的长等于点D到平面PBC的距离.而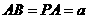 ,∴
,∴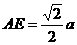 .………5分
.………5分
 即点D到平面PBC的距离为
即点D到平面PBC的距离为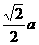 .………………6分
.………………6分
(Ⅱ) ∵PA⊥底面ABCD,∴平面PAD⊥底面ABCD,
引CM⊥AD于M,MN⊥PD于N,则CM⊥平面PAD,
∴MN是CN在平面PAD上的射影,
由三垂线定理可知CN⊥PD,
∴∠CNM是二面角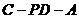 的平面角.…………9分
的平面角.…………9分
依题意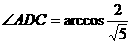 ,
,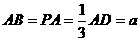 ,
,
∴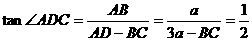 ,∴
,∴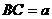 ,
,
可知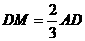 ,∴
,∴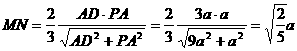 ,
,
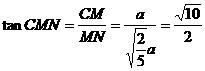 ,∴二面角
,∴二面角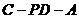 的大小为
的大小为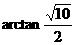 …… 12分
…… 12分
解法二:如图, A为原点,分别以AD、AB、AP为x轴、y轴、z轴建立空间直角坐标系.
 (Ⅰ)依题意
(Ⅰ)依题意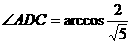 ,
,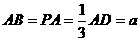 ,
,
∴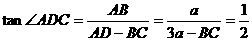 ,
,
∴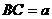 . 则
. 则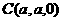 ,
,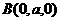 ,
,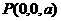 ,
,
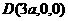 ,
,
∴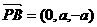 ,
,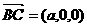 ,
,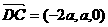 .
.
设平面PBC的一个法向量为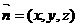 ,则
,则
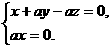 令
令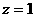 ,得
,得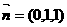 ,
,
则点D到平面PBC的距离等于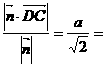
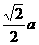 .……………6分
.……………6分
(Ⅱ) ∵AB⊥PA,AB⊥AD,∴AB⊥底面PDA,∴平面PDA的一个法向量为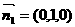 .
.
设平面PDC的一个法向量为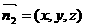 ,
,
∵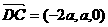 ,
,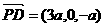 ,∴
,∴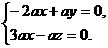
令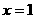 ,得
,得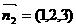 ,∴
,∴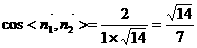 .
.
∵二面角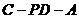 是锐二面角,∴二面角
是锐二面角,∴二面角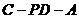 的大小为
的大小为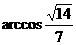 .……12分
.……12分
18.(本小题满分12分)平面内有向量=(1,7),=(5,1),=(2,1),点Q为直线OP上的一个动点.
(1)当·取最小值时,求的坐标;
(2)当点Q满足(1)的条件和结论时,求cos∠AQB的值.
解:设=(x.y),∵与共线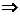 x=2y. ∴=(2y,y),又=-=(1―2y,7―y),
x=2y. ∴=(2y,y),又=-=(1―2y,7―y),
=-=(5―2y,1―y).
∴·=(1―2y)(5―2y)+(7―y)(1―y) =5y2-20y+12
 =5(y―2)2―8≥―8.此时y=2,=(4,2).
=5(y―2)2―8≥―8.此时y=2,=(4,2).
(2)当=(4,2)时,=(-3,5),=(1,-1),
·=-8.
∴cos∠AQB===-.
17. (本小题满分12分)某校的一个研究性学习小组进行一种验证性实验,已知该种实验每次实验成功的概率为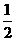 .
.
(1)求他们做了5次这种实验至少有2次成功的概率;
(2)如果在若干次实验中累计有两次成功就停止实验,否则将继续进行下次实验,但实验的总次数最多不超过5次,求该小组做实验的次数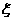 的概率分布列和期望.
的概率分布列和期望.
解:(1)设5次实验中,只成功一次为事件A,一次都不成功为事件B,至少2次成功为事件C,则
P(C)=1-P(A+B)=1-P(A)-P(B)------------------2分
=1- =
=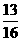
所以5次实验至少2次成功的概率为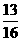 .---------------------5分
.---------------------5分
(2) 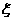 的可能取值为2,3,4,5.
的可能取值为2,3,4,5.
又∵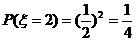 ;
;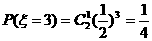
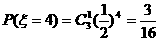
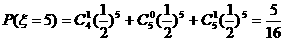 -----------9分
-----------9分
(每对一个得1 分)
∴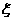 的分布列为:
的分布列为:
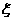 |
2 |
3 |
4 |
5 |
|
P |
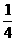 |
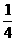 |
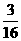 |
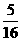 |
----------------------------10分
∴Eξ=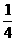 ×2+
×2+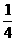 ×3+
×3+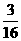 ×4+
×4+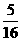 ×5=
×5=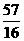 -------------------------12分
-------------------------12分
16.(本小题满分12分)已知向量=(cos4x,-1),=(1,cin4x+sin2x),x∈R,f(x)=·.
(1)求函数f(x)的最小正周期; (2)若x∈[0, ],求f(x)的最值及相应的x值.
解:f(x)=·=cos4x―sin4x―sin2x=cos2x-sin2x=2cos(2x+).
(1)函数f(x)的最小正周期T=π.
(2).∵x∈[0, ]∴2x+∈[,].
∴当2x+=即x=0时,f(x)mox=1.
当2x+=π即x=时,f(x)min=-2.
15.设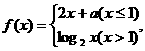 若
若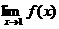 存在,则常数
存在,则常数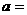 __-2 .
__-2 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com