
题目列表(包括答案和解析)
4.设向量 =(-1,2),
=(-1,2),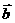 =(2,-1),则(
=(2,-1),则( ·
·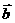 )(
)( +
+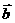 )等于B A(1,1)B(-4,-4) C-4D(-2,-2)
)等于B A(1,1)B(-4,-4) C-4D(-2,-2)
8)已知向量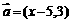 ,
,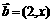 ,且
,且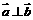 ,则由
,则由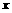 的值构成的集合是CA.
的值构成的集合是CA.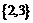 B.
B.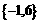 C.
C.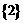 D.
D.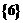
(8)已知向量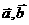 ,且
,且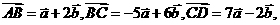 则一定共线的A(A) A、B、D
(B) A、B、C
(C) B、C、D (D)A、C、D 6.已知向量
则一定共线的A(A) A、B、D
(B) A、B、C
(C) B、C、D (D)A、C、D 6.已知向量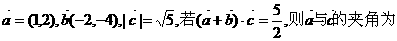 (C )A.30° B.60° C.120° D.150°
(C )A.30° B.60° C.120° D.150°
2. 已知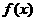 对于任意实数
对于任意实数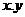 满足
满足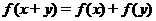 ,当
,当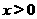 时,
时,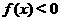
(1) 求证
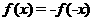
(2) 判断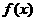 的单调性
的单调性
证明
(1)令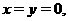 得
得
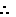
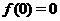
-
令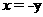 ,得
,得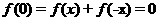
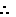
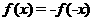
(2)设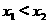 ,则
,则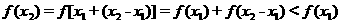
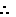
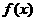 在R上是单调函数
在R上是单调函数
变题 1. 已知函数是定义R在上的增函数,且满足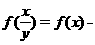

(1) 求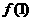 的值
的值
(2) 若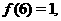 解不等式
解不等式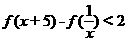
解 (1) 令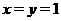 ,得
,得
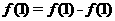
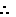
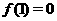 -
-
(3) 在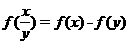 中,令
中,令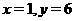 得
得
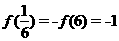
从而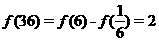

又原不等式可化为
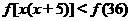 ,
,
且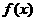 是
是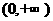 上的增函数,
上的增函数,
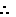 原不等式等价于
原不等式等价于
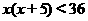
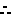
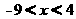
又 
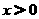
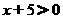
解得 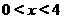
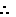
 原不等式的解集为(0,4)
原不等式的解集为(0,4)
1. 已知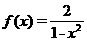 (
(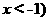 ,求
,求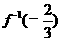 的值
的值
解法1 先求反函数
由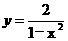 得
得
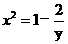

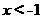

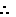
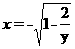 且
且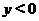
故原函数的反函数是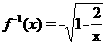
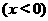
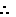
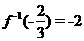
解法2从互为反函数的函数的关系看
令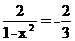 解得
解得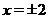


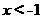
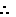
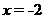
即
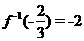
变题
3、作差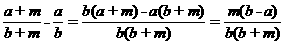
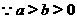 ,
,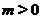
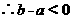
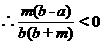
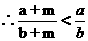
一 题 多 解
已知数列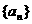 满足
满足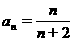 ,
,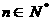 ,试比较
,试比较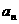 与
与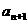 的大小
的大小
方法一:作差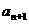 -
-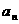 =
=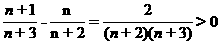 ,
,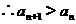
方法二:作商
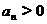


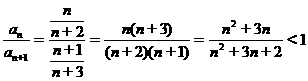
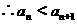 -
-
方法三:(单调性)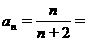
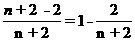 ,
,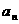 关于
关于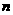 单调递增
单调递增
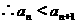
方法四:浓度法 把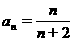 看成是一杯溶液(糖)的浓度,随着
看成是一杯溶液(糖)的浓度,随着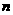 的增大(相当于向溶液中加糖),浓度 当然增大,易得
的增大(相当于向溶液中加糖),浓度 当然增大,易得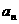

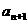
2、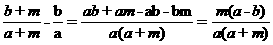 -
-
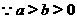 ,
,
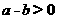 ,又
,又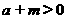

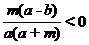 ,
, 
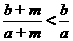 -
-
1、
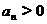

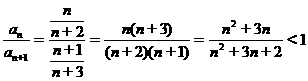
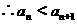
3、已知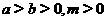 ,求证:
,求证: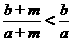
解: 原题:证明:作差-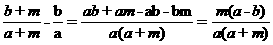 ‘
‘
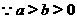 ,
,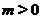
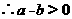
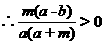
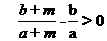
2、已知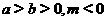 ,且
,且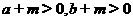 ,求证:
,求证:
1、已知数列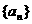 满足
满足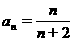 ,
,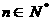 ,试比较
,试比较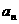 与
与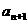 的大小
的大小
2、当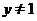 时
时
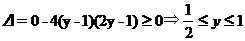
所以函数的值域为[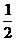 ,1
,1
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com