
题目列表(包括答案和解析)
2.下列各式中,对任何实数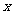 都成立的一个是
都成立的一个是
(A) 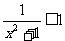 (B)
(B) 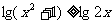 (C)
(C) 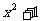
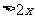 (D)
(D) 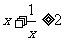
1.已知集合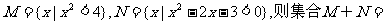
A.{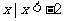 }
B.{
}
B.{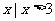 } C.{
} C.{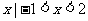 } D. {
} D. {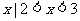 }
}
例1(1)已知c<b<a,且ac<0,那么下列选项中一定成立的是
(A)ab>ac (B)c(b-a)<0 (C)cb2<ab2 (D)ac(a-c)>0
(2)若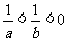 。则下列不等式(1)a+b<ab (2)
。则下列不等式(1)a+b<ab (2) (3)a<b (4)
(3)a<b (4)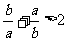 中,正确的有____个
中,正确的有____个
本题是运用不等式性质求解的基础题,(1)题选A (2)题填2。
例2不等式3x2-log
ax<0在区间(0,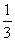 )内恒成立,求a的取值范围。
)内恒成立,求a的取值范围。
本题数形结合,借助两个函数图象比较两函数值的大小,答案: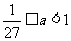
例3已知f(x)=x2-2ax+2,当 恒成立,求a的取值范围。
恒成立,求a的取值范围。
分析:f(x)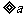 恒成立等价于f(x)min
恒成立等价于f(x)min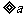 ,问题化归为求f(x)在
,问题化归为求f(x)在 上的最小值g(a),再解不等式g(a)
上的最小值g(a),再解不等式g(a) 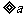 ,可求a的取值范围。
,可求a的取值范围。
例4.在约束条件 的取值范围是
.
的取值范围是
.
分析:画出约束条件所表示的可行域,目标函数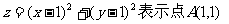 和可行域内点的距离的平方,最小值为点A到直线
和可行域内点的距离的平方,最小值为点A到直线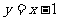 的距离的平方,最大值在点(2,0)处取得。答案为
的距离的平方,最大值在点(2,0)处取得。答案为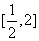 。
。
例5.已知二次函数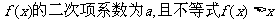 的解集为(1,2)
的解集为(1,2)
(1)若方程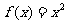 有两个相等的实根,求
有两个相等的实根,求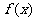 的解析式;
的解析式;
(2)若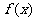 的最大值大于1,求a的取值范围.
的最大值大于1,求a的取值范围.
解:(1)不等式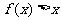 的解集为(1,2)
的解集为(1,2)

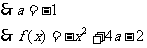
(2)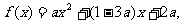
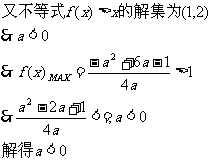
本题涉及“三个二次”,要引起足够重视。
例6.已知函数f(x)=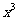 -
-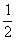 x2+bx+c.(1)若f (x)有极值,求b的取值范围;
x2+bx+c.(1)若f (x)有极值,求b的取值范围;
(2)当f (x)在x=1处取得极值时,
①若当x∈[-1,2]时,f (x)<c2恒成立,求c的取值范围;
②证明:对[-1,2]内的任意两个值x1,x2,都有|f (x1)-f (x2)|<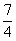 .
.
解:(1)∵f(x)=x3-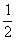 x2+bx+c, ∴f `(x)=3x2-x+b
x2+bx+c, ∴f `(x)=3x2-x+b
要使f(x)有极值,则f `(x)=3x2-x+b=0有实数解
从而△=1-12b≥0,∴b≤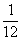 而当b=
而当b=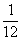 时,函数在R上严格递增,∴b<
时,函数在R上严格递增,∴b<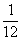
(2)∵f(x)在x=1处取得极值 ∴f `(1)=3-1+b=2+b=0 ∴b=-2
①∴f(x)=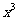 -
-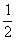 x2-2x+c
x2-2x+c
∵f `(x)=3x2-x-2=(3x+2)(x-1)
∴当x∈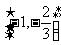 时,f `(x)>0,函数单调递增
时,f `(x)>0,函数单调递增
当x∈(-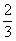 ,1)时,f `(x)<0,函数单调递减
,1)时,f `(x)<0,函数单调递减
∴当x=-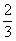 时,f (x)有极大值
时,f (x)有极大值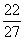 +c
+c
又f (2)=2+c >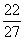 +c, f (-1)=
+c, f (-1)=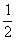 +c<
+c<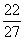 +c
+c
∴x∈[-1,2]时,f (x)最大值为f (2)=2+c
∴c2>2+c ∴c<-1或c>2
②由上可知,当x=1时,f(x)有极小值-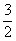 +c
+c
又f (2)=2+c>-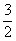 +c, f (-1)=
+c, f (-1)=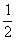 +c>-
+c>-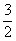 +c
+c
∴x∈[-1,2]时,f (x)的最小值为-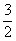 +c
+c
∴|f
(x1)-f (x2)|<|fmax(x)-fmax(x)|=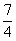 ,故结论成立.
,故结论成立.
涉及函数的增减区间,最大值与最小值与不等式也紧密相关。
不等式重点考查的有四种题型:解不等式,证明不等式,不等式的应用,不等式的综合性问题。突出不等式的知识在解决实际问题中的应用价值,借助不等式来考查学生的应用意识是考试重点。不等式的证明是考试难点。
强调对实际问题的抽象,特别强调一元二次不等式的有关问题,新增了“设计求解的程序框图”;去掉了“含绝对值的不等式.”及“三角不等式| a|-|b|≤|a+b|≤|a|+|b|”。
4.基本不等式: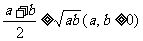
(1)了解基本不等式的证明过程。
(2)会用基本不等式解决简单的最大(小)值问题。
3.二元一次不等式组与简单线性规划问题
(1)会从实际情景中抽象出二元一次不等式组。
(2)了解二元一次不等式组的几何意义,能用平面区域表示二元一次不等式组。
(3)会从实际情景中抽象出一些简单的二次线性规划问题,并能加以解决。
2.一元二次不等式
(1)会从实际情景中抽象出一元二次不等式模型。
(2)通过函数图像了解一元二次不等式与相应的二次函数,一元二次方程的联系。
(3)会解一元二次不等式,对给定的一元二次不等式,会设计求解的程序框图。
1.不等关系
了解现实世界和日常生活中的不等关系,了解不等式(组)的实际背景。
16、已知函数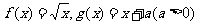 .
(1) 求
.
(1) 求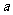 的值,使点
的值,使点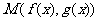 到直线
到直线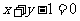 的距离最短为
的距离最短为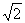 ;
(2) 若不等式
;
(2) 若不等式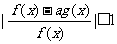 在
在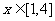 恒成立,求
恒成立,求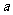 的取值范围.
的取值范围.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com